Introduction#

In this post, I’ll present my write-ups for some of the challenges listed in the crypto category, in no particular order.
The challenges are:
I didn’t manage to solve two of them, but I will briefly give my thoughts on them.
Shuffled#
Play on HackropoleDifficulty :
Points : 100
Solves : 490
Description :
Uh oh, we mixed up the characters of the flag. Can you put them back in the right order?
The following source code was provided :
import random
flag = list(open("flag.txt", "rb").read().strip())
random.seed(random.randint(0, 256))
random.shuffle(flag)
print(bytes(flag).decode())
# f668cf029d2dc4234394e3f7a8S9f15f626Cc257Ce64}2dcd93323933d2{F1a1cd29db
This one doesn’t need much explanations.
Basically, we can test all 256 seed values and shuffle an ordered list from 0 to 70 (the length of the flag).
This will produce a shuffled list, whose elements represent the original index of the flag. We can reconstruct the real flag from this list.
If the guessed seed was correct, the flag should start with “FCSC{”.
The full script is given below :
import random
flag = list(open("output.txt", "rb").read().strip())
for i in range(256):
a = list(range(len(flag)))
random.seed(i)
random.shuffle(a)
# build a dict with shuffled indexes
f = {}
for j, e in enumerate(a):
f[e] = flag[j]
# unshuffle flag
m = []
for j in range(len(flag)):
m.append(f[j])
f = bytes(m).decode()
if f.startswith('FCSC'):
print(f)
FCSC{d93d32485aec7dc7622f13cd93b922363911c36d2ffd4f829f4e3264d0ac6952}

My Tailor is Rich#
Play on HackropoleDifficulty :
Points : 224
Solves : 134
Description :
Your colleagues, experts in reverse engineering, have reconstructed a password encoding algorithm of one specific equipment. They suspect that it is cryptographically weak but they need your help to prove it.
The source code of the service was provided :
import string
import random
N = 8
def encode(pwd):
def F(tmp):
if tmp % 2:
return (tmp % 26) + ord('A')
else:
r = tmp % 16
if r < 10:
return ord('0') + r
else:
return r - 10 + ord('A')
a, res = 0, []
for i in range(len(pwd)):
P, c, S = pwd[:i], pwd[i], pwd[i+1:]
S1, S2, T = sum(P), sum(S), sum(pwd)
a = F((a + c) * i + T)
res.append(a)
return bytes(res)
def get_random_string(length):
return ''.join(random.choice(string.ascii_letters) for _ in range(length)).encode()
pwd = get_random_string(8)
enc = encode(pwd)
print(f'Can you find {N} different passwords that encode to "{enc.decode()}"?')
P = []
S = [enc]
try:
for _ in range(N):
p = input(">>> ").encode()
if not p.isascii():
print("Please enter only ASCII strings.")
exit(1)
P.append(p)
S.append(encode(p))
if len(set(P)) == N and len(set(S)) == 1:
print("Congrats!! Here is your flag:")
print(open("flag.txt").read())
else:
print("Nope!")
except:
pass
The challenge description indicates that this encoding algorithm has been recovered from some kind of equipment.
I don’t know if this particular encoding was used in the real world or not, but it doesn’t really matter for the resolution.
All characters of the encoded password are entirely dependent on the previous character. The first one is the function F applied to the sum of the ASCII values of the password.
Starting from the first character, we can progressively recover lists of valid password characters for each positions :
def getValid(t, prev, res):
m1 = []
# search candidates satisfying the relation
for i in (string.ascii_letters + string.digits).encode():
x = (res[prev] + i) * (prev+1) + t
if F(x) == res[prev+1]:
m1.append(i)
# limit to 3 results as it's enough
return m1[:3]
The above function needs a possibility for the sum of the password characters t. We can build a dictionary mapping the values x to F(x) and use that to find some potential sum values :
DEC = {}
for i in range(1024):
if DEC.get(F(i)):
DEC[F(i)].append(i)
else:
DEC[F(i)] = [i]
After having gathered 7 lists of potential password characters for each position, the last step is to find all the last ones, that with any combination of the potential password characters, will produces the expected sum :
def solve(res):
Ts = DEC[res[0]]
pwd = []
for t in Ts:
m1 = getValid(t, 0, res)
m2 = getValid(t, 1, res)
m3 = getValid(t, 2, res)
m4 = getValid(t, 3, res)
m5 = getValid(t, 4, res)
m6 = getValid(t, 5, res)
m7 = getValid(t, 6, res)
for i in (string.ascii_letters + string.digits).encode():
for r in itertools.product(m1, m2, m3, m4, m5, m6, m7):
if sum(r) + i == t:
pwd.append([i]+list(r))
return pwd
This quickly produces several dozens of passwords encoding to the same result.
The full solve script is given below :
import string
import itertools
from pwn import remote
def F(tmp):
if tmp % 2:
return (tmp % 26) + ord('A')
else:
r = tmp % 16
if r < 10:
return ord('0') + r
else:
return r - 10 + ord('A')
def getValid(t, prev, res):
m1 = []
# search candidates satisfying the relation
for i in (string.ascii_letters + string.digits).encode():
x = (res[prev] + i) * (prev+1) + t
if F(x) == res[prev+1]:
m1.append(i)
# limit to 3 results as it's enough
return m1[:3]
def solve(res):
Ts = DEC[res[0]]
pwd = []
for t in Ts:
m1 = getValid(t, 0, res)
m2 = getValid(t, 1, res)
m3 = getValid(t, 2, res)
m4 = getValid(t, 3, res)
m5 = getValid(t, 4, res)
m6 = getValid(t, 5, res)
m7 = getValid(t, 6, res)
for i in (string.ascii_letters + string.digits).encode():
for r in itertools.product(m1, m2, m3, m4, m5, m6, m7):
if sum(r) + i == t:
pwd.append([i]+list(r))
return pwd
DEC = {}
for i in range(1024):
if DEC.get(F(i)):
DEC[F(i)].append(i)
else:
DEC[F(i)] = [i]
conn = remote("challenges.france-cybersecurity-challenge.fr", 2100)
conn.recvuntil(b'to "')
expected = conn.recvuntil(b'"', drop=True)
conn.recvline()
for e in solve(expected)[:8]:
e = bytes(e)
conn.sendline(e)
conn.recvuntil(b"flag")
conn.recvline()
print(conn.recvline())
conn.close()
FCSC{515dd8416571401f2f0bf039e9adeec0cb9c51f4430923baa9fcb3fa13e14091}
T-Rex#
Play on HackropoleDifficulty :
Points : 344
Solves : 67
Description :
Simply decrypt the flag :-)
The following source code was provided :
import os
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
class TRex:
def __init__(self, key):
N = len(key)
M = 2 ** (8 * N)
self.key = key
self.iv = int.from_bytes(key, "big")
R = lambda x: ((2 * x + 1) * x)
for _ in range(31337):
self.iv = R(self.iv) % M
self.iv = int.to_bytes(self.iv, N, "big")
def encrypt(self, data):
E = AES.new(self.key, AES.MODE_CBC, iv = self.iv)
return self.iv + E.encrypt(pad(data, 16))
if __name__ == "__main__":
E = TRex(os.urandom(16))
flag = open("flag.txt", "rb").read().strip()
c = E.encrypt(flag)
print(c.hex())
# 070a4a5811dd013c301f30070924528796cb8fe8ddd6d8851f90ab1a8977e9c71accbed0a5936414445739ce76763002fd29337834c8976fef36decdc522a6b93c967c90d0e69e46674d634ba5a9badbd834bad8042515029b6fa833c98da0a7
The flag is encrypted using AES128-CBC. The IV is derived from the encryption key by applying the transformation R 31337 times, modulo $2^{128}$.
The goal is clearly to recover the encryption key from the IV and decrypt the flag.
After playing a bit with the transformation R, I realized that applying it M/2 times to a value x produces x again. This makes sense as M is a power of 2, so the order of the group generated by R is at most M/2.
But because $M = 2^{128}$, naivly applying the transformation R to the IV $2^{127}-31337$ times would be infeasible in a reasonable amount of time.
It’s possible apply the transformation in a smart way, by first defining 128 intermediary transformation for each power of 2 :
R2 = R(R(x))
R4 = R2(R2(x))
...
Then, for each bit of the number of times we need to apply R, we can apply the corresponding intermediary transformation. For example, applying R 10 times is done like this : R8(R2(x))
The full attack is given in the script below:
from Crypto.Cipher import AES
from sage.all import *
# Build the intermediary transformations
p = PolynomialRing(Zmod(2**128), "x")
x = p.gen()
rs = [2*x**2 + x]
for i in range(1, 128):
r0 = rs[i-1]
ri = r0(r0(x))
rs.append(ri)
# recover the key
m = 0x070a4a5811dd013c301f300709245287
b = bin(2**127 - 31337)[2:].zfill(128)[::-1]
for i, e in enumerate(b):
if e == "1":
m = rs[i](m)
key = int(m)
key = int.to_bytes(key, 16, "big")
E = AES.new(key, AES.MODE_CBC, iv=bytes.fromhex("070a4a5811dd013c301f300709245287"))
print(E.decrypt(bytes.fromhex("96cb8fe8ddd6d8851f90ab1a8977e9c71accbed0a5936414445739ce76763002fd29337834c8976fef36decdc522a6b93c967c90d0e69e46674d634ba5a9badbd834bad8042515029b6fa833c98da0a7")))
FCSC{54a680c151c2bff32fd2fdc12b4f8558012dc71e429f075bab6bfc0322354bf4}
Gaston La Paffe#
Play on HackropoleDifficulty :
Points : 429
Solves : 29
Description :
Gaston works in a public administration. He spends his time processing various letters. He finds that his job is not paid at its fair value: it has been more than 10 years that he did not have a single bonus while he only takes three naps a day! To top it all off, among all the letters he has processed over the years, he has seen more than 500 bonus notifications for his colleagues!
Unfortunately, all these notifications are signed with an innovative method invented by the HR departement. Only this departement has the private key to sign.
Gaston wrote his ideal bonus letter. If there were a way to add HR’s digital signature to it, he would slip his notification in with the others, and would receive his bonus!
It looks like there’s a leak in the signature method. Gaston is counting on you to help him find the signing key used by the HR departement.
The following source code was provided :
import os
import json
import hashlib
import string
import numpy as np
from Crypto.Random.random import randint, choice
from Crypto.Hash import SHA512, SHA256
from Crypto.Util.number import bytes_to_long
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
Q = 8383489
B = 16384
N = 512
class Server:
def __init__(self, Q, B, N):
self.Q = Q
self.B = B
self.N = N
self.a = [randint(0, Q - 1) for _ in range(self.N)]
self.__s1 = [randint(-1, 1) % Q for _ in range(self.N)]
self.__s2 = [randint(-1, 1) % Q for _ in range(self.N)]
self.t = self.poly_mul_add(self.a, self.__s1, self.__s2)
def sk(self):
return self.__s1, self.__s2
def pk(self):
return self.a, self.t
def H(self, v1, m):
h = bytes_to_long(SHA512.new(str(v1).encode() + m).digest())
h = list(map(int, list(f"{h:0512b}")))
return h
def poly_add(self, p1, p2):
return [ (p1[i] + p2[i]) % self.Q for i in range(self.N) ]
def poly_sub(self, p1, p2):
return [ (p1[i] - p2[i]) % self.Q for i in range(self.N) ]
def poly_mul_add(self, p1, p2, p3):
return self.poly_add(self.poly_mul(p1, p2), p3)
def poly_mul(self, p1,p2):
res = np.convolve(p1, p2)
res = [0] * (2 * self.N - 1 - len(res)) + list(res)
a = list(map(int, res[:self.N]))
b = list(map(int, res[self.N:] + [0]))
res = self.poly_sub(a, b)
return res
def reject(self, z):
for v in z:
if v > self.B and v < self.Q - self.B:
return True
return False
def sign(self, m):
while True:
y1 = [ randint(-self.B, self.B) % self.Q for _ in range(self.N) ]
y2 = [ randint(-self.B, self.B) % self.Q for _ in range(self.N) ]
h = self.poly_mul_add(self.a, y1, y2)
c = self.H(h, m)
z1 = self.poly_mul_add(self.__s1, c, y1)
z2 = self.poly_mul_add(self.__s2, c, y2)
if self.reject(z1) or self.reject(z2):
continue
return y1, z1, z2, c
def verify(self, z1, z2, c, m):
if self.reject(z1) or self.reject(z2):
return False
temp1 = self.poly_mul_add(self.a, z1, z2)
temp2 = self.poly_mul(self.t, c)
h = self.poly_sub(temp1, temp2)
c_prime = self.H(h, m)
return c == c_prime
def get_random_string(length):
return ''.join(choice(string.ascii_letters) for _ in range(length))
if __name__ == "__main__":
server = Server(Q, B, N)
a, t = server.pk()
print(json.dumps({
"a": a,
"t": t,
}))
data = []
for i in range(N):
message = get_random_string(20)
y1, z1, z2, c = server.sign(message.encode())
assert server.verify(z1, z2, c, message.encode()), "Error: verification error."
data.append({
"message": message,
"z1": z1,
"z2": z2,
"c": c,
"y1": y1,
})
print(json.dumps(data))
flag = open("flag.txt", "rb").read()
s1, s2 = server.sk()
key = SHA256.new(str(s1).encode() + str(s2).encode()).digest()
iv = os.urandom(16)
E = AES.new(key, AES.MODE_CBC, iv = iv)
enc = E.encrypt(pad(flag, 16))
print(json.dumps({
"iv": iv.hex(),
"enc": enc.hex()
}))
# {"a": [1632237, 5378119, ..., 3632408, 7304636], "t": [3921273, 7249125, ..., 8116376, 2704116]}
# [{"message": "LQmgRMudiUzGASyJsWCB", "z1": [15703, 8367671, ..., 8376696, 8374031], "z2": [8378515, 999, ..., 8377917, 8375870], "c": [0, 1, 0, 0, ..., 1, 0, 0], "y1": [15700, 7467, ..., 8376672, 8374039]}, {...}]
# {"iv": "21171db2bbe684a8afb6c9f81b43c634", "enc": "d258ee201e92ddaaac0dc435639986dd8e1e1f44927bef6e10d9da365aefc6524727bd5e5df11010e9d23d97cd839cb3941c38584c796c6037edc4f4f418e3ab11bbee787b4a7117457704f67ae127da"}
We are given a public key and 500 signatures. Our goal is to recover the private key. The algorithm itself is unknown and judging from the challenge’s description might even be custom, but it seems to be inspired by a real post quantum cryptographic signature scheme.
Based on the function names I realised that we are working with polynomials.

To be more precise we are working in $\mathbb{Z}_Q[x]/(x^{512}+1)$ with $Q=8383489$, and in this ring the multiplication of polynomials is equal to their convolution.
The private key is composed of two elements, $s_1$ and $s_2$. Both are polynomials with 512 random coefficients taken between -1 and 1.
The public key is also composed of two elements :
- $a$ : A polynomial with 512 random coefficients taken between 0 and
Q-1; - $t = as_1 + s_2$
A signature is composed of three elements:
- $c$ : A polynomial whose coefficients represent the SHA-512 hash of the message to sign;
- $z_1 = cs_1 + y_1$, with $y_1$ being a polynomial with 512 random coefficients taken between -16384 and 16384;
- $z_2 = cs_2 + y_2$, with $y_2$ constructed in the same way as $y_1$.
The description indicates that there is a leak in the signature process and in fact, the function sign also returns the component $y_1$. That’s quite a big leak actually !
With the knowledge of a signature $(c, z_1, z_2)$, the public key $(a, t)$ and the leak corresponding to this signature $(y1)$ we can easily recompute the private key $(s1, s2)$ :
- $s_1 = (z_1 - y_1) * c^{-1}$
- $s_2 = t - (a * s_1)$
The only requirement is being able to compute the modular inverse of a polynomial, which is not implemented in the provided code, but sage can do that pretty easily.
The full script is given below:
import json
from sage.all import *
from Crypto.Hash import SHA256
from Crypto.Cipher import AES
from Crypto.Util.Padding import unpad
def top(r):
# convert a list to a polynom
a = 0
for i,e in enumerate(r):
a += e*x**i
return a
def getSk(y1, z1, z2, c, t, a):
z1 = top(z1)
z2 = top(z2)
y1 = top(y1)
t = top(t)
a = top(a)
c = top(c)
s1c = z1- y1
s1 = (s1c * c.inverse_mod(x**512+1)).mod(x**512+1)
s2 = (t - (a * s1)).mod(x**512+1)
s1 = s1.coefficients(sparse=false)
s2 = s2.coefficients(sparse=false)
return s1, s2
Q = 8383489
flag_data = None
Traces = None
Pub = None
with open("output.txt", "r") as f:
a, b, c = f.readlines()
Pub = json.loads(a)
Traces = json.loads(b)
flag_data = json.loads(c)
a = Pub["a"]
t = Pub["t"]
p = PolynomialRing(Zmod(Q), "x")
x = p.gen()
sig = Traces[0]
s1, s2 = getSk(sig["y1"], sig["z1"], sig["z2"], sig["c"], t, a)
key = SHA256.new(str(s1).encode() + str(s2).encode()).digest()
iv = bytes.fromhex(flag_data["iv"])
flag = bytes.fromhex(flag_data["enc"])
E = AES.new(key, AES.MODE_CBC, iv = iv)
print(unpad(E.decrypt(flag), 16).decode())
FCSC{c3b929519b28954612bf81af628dd93b6adef1e79539887729e1a2a27569eeb0}
Surface#
Play on HackropoleDifficulty :
Points : 477
Solves : 10
Description :
This script generates an AES key in an exotic way, then protects the flag with it. Can you recover this key?
The following source code was provided :
import os
import json
import gmpy2
from fractions import Fraction
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
def encrypt(n):
IV = os.urandom(16)
FLAG = open("flag.txt", "rb").read()
k = int.to_bytes(n, 32, "big")
aes = AES.new(k, AES.MODE_CBC, iv = IV)
ctxt = aes.encrypt(pad(FLAG, 16))
output = {
"iv": IV.hex(),
"ciphertext": ctxt.hex(),
}
return output
if __name__ == "__main__":
try:
a = Fraction(input(">>> a = "))
b = Fraction(input(">>> b = "))
c = a ** 2 + b ** 2
assert gmpy2.is_square(c.numerator)
assert gmpy2.is_square(c.denominator)
assert a * b == 20478
n = int(gmpy2.isqrt(c.numerator))
output = encrypt(n)
print(json.dumps(output))
except:
print("Error: check your inputs.")
# {"iv": "a79ec4a60d33eae0e0d9e06f8b309348", "ciphertext": "29d4c8dceecb461cfc7c06242d25879cdcf47fca47ded512ea830d09613ecd497a9720231cb423e95ed2463f5f74d8f5c4c9b75704ff738fe48475191b62f14280f32c05daf9300ab1d692d8717371dc"}
After a lot of research online, this problem is known as the congruent number problem.
The goal is to find two rational sides of a triangle so that the area is equal to 10239.
What does this have to do with crypto you might wonder. The answer is : Elliptic curves !

I must admit, I didn’t find the relation with elliptic curves until several hours of searching.
Starting with the two equations of the problem: $a^2 + b^2 = c^2$ and $\frac{1}{2}ab = n$. If you set $x = \frac{n(a+c)}{b}$ and $y = \frac{2n^2(a+c)}{b^2}$, you can derive the equation of an Elliptic curve :
$$y^2 = x^3 - n^2x$$
Converting a point back to triangle sides can be done by computing $a = \frac{(x^2 - n^2)}{y}$ and $b = \frac{2nx}{y}$.
Solving the congruent number problem is equivalent to finding integral points on the above curve, whose Y-coordinates are non-zero.
Thankfully sage has a builtin function for that ! Let’s try it :
E = EllipticCurve([-5**2, 0])
E.integral_points()
# [(-5 : 0 : 1), (-4 : 6 : 1), (0 : 0 : 1), (5 : 0 : 1), (45 : 300 : 1)]
If we convert the points (-4, 6) and (45, 300) to sides of the triangle, we get:
from fractions import Fraction
def convert(x, y, n):
a = abs(x**2-n**2)
b = abs(2*n*x)
a = Fraction(f"{a}/{y}")
b = Fraction(f"{b}/{y}")
return a, b
convert(-4, 6, 5)
# (Fraction(3, 2), Fraction(20, 3))
convert(45, 300, 5)
# (Fraction(20, 3), Fraction(3, 2))
This is exaclty the expected results. We just have to do that for the challenge value.
E = EllipticCurve([-10239**2, 0])
E.integral_points()
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
/usr/lib/python3/dist-packages/sage/schemes/elliptic_curves/ell_rational_field.py in integral_points(self, mw_base, both_signs, verbose)
5810 try:
-> 5811 mw_base = self.gens()
5812 except RuntimeError:
/usr/lib/python3/dist-packages/sage/schemes/elliptic_curves/ell_rational_field.py in gens(self, proof, **kwds)
2229
-> 2230 gens, proved = self._compute_gens(proof, **kwds)
2231 self.__gens = (gens, proved)
/usr/lib/python3/dist-packages/sage/schemes/elliptic_curves/ell_rational_field.py in _compute_gens(self, proof, verbose, rank1_search, algorithm, only_use_mwrank, use_database, descent_second_limit, sat_bound)
2337 del self.__mwrank_curve
-> 2338 raise RuntimeError("Unable to compute the rank, hence generators, with certainty (lower bound=%s, generators found=%s). This could be because Sha(E/Q)[2] is nontrivial."%(C.rank(),G) + \
2339 "\nTry increasing descent_second_limit then trying this command again.")
RuntimeError: Unable to compute the rank, hence generators, with certainty (lower bound=0, generators found=[]). This could be because Sha(E/Q)[2] is nontrivial.
Try increasing descent_second_limit then trying this command again.
During handling of the above exception, another exception occurred:
RuntimeError Traceback (most recent call last)
<ipython-input-1-0352cc7046c9> in <module>
1 E=EllipticCurve([-Integer(10239)**Integer(2), Integer(0)])
----> 2 E.integral_points()
/usr/lib/python3/dist-packages/sage/schemes/elliptic_curves/ell_rational_field.py in integral_points(self, mw_base, both_signs, verbose)
5811 mw_base = self.gens()
5812 except RuntimeError:
-> 5813 raise RuntimeError("Unable to compute Mordell-Weil basis of {}, hence unable to compute integral points.".format(self))
5814 r = len(mw_base)
5815 else:
RuntimeError: Unable to compute Mordell-Weil basis of Elliptic Curve defined by y^2 = x^3 - 104837121*x over Rational Field, hence unable to compute integral points.
Well… Let’s use Magma then :
E := EllipticCurve([-10239*10239, 0]);
IntegralPoints(E);
# [ (-10239 : 0 : 1), (0 : 0 : 1), (10239 : 0 : 1) ]
# [ <(-10239 : 0 : 1), 1>, <(0 : 0 : 1), 1>, <(10239 : 0 : 1), 1> ]
No crash, but no results either… Same with Pari/GP…

Back to the beginning !
After a lot of hours searching for another solution, I stumbled upon this paper, which gives another way to compute such points in section 4 :
N = 10239
E = EllipticCurve([-N*N, 0])
pari(E).ellheegner()
# 737343773862301088045509418793921869066076/10893159238600577313677917228652511841, 625862116444448047393458603029555713662450024330982757172975030/35952639365198540562613869494033558726733788804390127889
The above computation took only 3 hours to give a result.
From the result of ellheegner we just need to convert both fractions to sides of the triangle.
The full solution script is given below :
from sage.all import gcd, QQ
from fractions import Fraction
import gmpy2
from Crypto.Cipher import AES
def decrypt(x, y):
a = Fraction(x)
b = Fraction(y)
c = a*a + b*b
n = int(gmpy2.isqrt(c.numerator))
k = int.to_bytes(n, 32, "big")
iv = bytes.fromhex("a79ec4a60d33eae0e0d9e06f8b309348")
flag = bytes.fromhex("29d4c8dceecb461cfc7c06242d25879cdcf47fca47ded512ea830d09613ecd497a9720231cb423e95ed2463f5f74d8f5c4c9b75704ff738fe48475191b62f14280f32c05daf9300ab1d692d8717371dc")
aes = AES.new(k, AES.MODE_CBC, iv=iv)
print(aes.decrypt(flag))
# https://arxiv.org/pdf/2106.07373.pdf
N = 10239
# E = EllipticCurve([-N*N, 0])
# pari(E).ellheegner()
# 737343773862301088045509418793921869066076/10893159238600577313677917228652511841, 625862116444448047393458603029555713662450024330982757172975030/35952639365198540562613869494033558726733788804390127889
# s/t, u/v
s = QQ(737343773862301088045509418793921869066076)
t = QQ(10893159238600577313677917228652511841)
u = QQ(625862116444448047393458603029555713662450024330982757172975030)
v = QQ(35952639365198540562613869494033558726733788804390127889)
x = abs(s/t)
y = abs(u/v)
a = abs(x**2 - N**2)
b = 2*N*x
g_a = gcd(a,y);
g_b = gcd(b, y);
a = a/g_a;
d = y/g_a;
b = b/g_b;
e = y/g_b;
print(a, b, d, e)
decrypt(f"{a}/{d}", f"{b}/{e}")
FCSC{67084c2bc8acfbf5e8a0d5e2809e230d092ab56630713dbe33ca42b8430a992b}
Hash-ish#
Play on HackropoleDifficulty :
Points : 336
Solves : 71
Description :
Do you know how Python
hashfunction actually works?
The following source code was provided :
#!/usr/bin/env python3.9
import os
try:
flag = open("flag.txt", "rb").read()
assert len(flag) == 70
flag = tuple(os.urandom(16) + flag)
challenge = hash(flag)
print(f"{challenge = }")
a = int(input(">>> "))
b = int(input(">>> "))
if hash((a, b)) == challenge:
print(flag)
else:
print("Try harder :-)")
except:
print("Error: please check your input")
This challenge was quite interesting as it consisted in finding a 2nd preimage for the Python hash function.
I hope everybody knows that this function is not cryptographically secure, but I never wondered if collisions are easy to produce.

The Python hash function behaves differently depending on the type of the object it is applied on :
hash(1337)
# 1337
hash((1337,))
# 1536106969631255485
hash("1337")
# -1803454164760456366
hash(b"1337")
# -1803454164760456366
For numbers it simply returns them modulo P = 2305843009213693951.
For tuples, which is the case in the challenge, it’s not that simple.
The source code of the hash function applied to tuples can be found here (Python 3.9).
Rewritten in Python, this gives :
def tupleHash(t):
acc = 2870177450012600261
for i in t:
acc += hash(i) * 14029467366897019727
acc %= 2**64
acc = ((acc << 31) | (acc >> 33))
acc %= (2 ** 64)
acc *= 11400714785074694791
acc %= (2 ** 64)
acc += len(t) ^ 2870177450012600261 ^ 3527539
acc %= (2 ** 64)
return acc
The only difference here is that the hash function returns signed integers, but this has no impact on the resolution :
tupleHash((1337, 88, 9))
# 11207200829502916047
hash((1337, 88, 9)) % 2**64
# 11207200829502916047
hash((1337, 88, 9))
# -7239543244206635569
The goal of the challenge is to find a tuple containing 2 integers (x, y), whose hash will produce the expected hash. In other words, we must find a 2nd preimage for this hash function.
Now that we have rewritten the function in Python, we can easily access the internal state. For example we could compute the internal state of the hash after having processed the first element :
def forwardHash(i):
# returns the internal state after having hashed 1 tuple element
acc = 2870177450012600261
acc += i * 14029467366897019727
acc %= 2**64
acc = ((acc << 31) | (acc >> 33))
acc %= (2 ** 64)
acc *= 11400714785074694791
acc %= (2 ** 64)
return acc
Knowing the internal state after the first step allows us to calculate the second tuple element that will produce the expected hash. This can be done by inverting the last hashing step, starting with the expected value. The inversion is possible because only additions, multiplications and rotations are used :
def reverseHash(expected, state):
# inverts the hashing process starting from an expected hash
# returns the second tuple element that will produce this hash
# based on the fact that the first element produced a given internal state
acc = expected
# only 2 elements
acc -= 2 ^ 2870177450012600261 ^ 3527539
acc %= (2 ** 64)
acc *= 614540362697595703
acc %= (2 ** 64)
acc = (acc & 0x7fffffff) << 33 | (acc >> 31)
acc %= 2 ** 64
acc -= state
acc % (2 ** 64)
acc *= 839798700976720815
return acc % (2 ** 64)
The strategy is simple. Choose an arbitrary small (< P) value as the first tuple element, compute the internal state and use it to compute the second element.
The only problem is that the second element y will likely be larger than P and as such hash(y) != y. In that case, we have to choose another value for x.
Finding a preimage was not too difficult in this scenario.
The full attack is implemented below :
#!/usr/bin/env python3.9
def forwardHash(i):
# returns the internal state after having hashed 1 tuple element
acc = 2870177450012600261
acc += i * 14029467366897019727
acc %= 2**64
acc = ((acc << 31) | (acc >> 33))
acc %= (2 ** 64)
acc *= 11400714785074694791
acc %= (2 ** 64)
return acc
def reverseHash(expected, state):
# inverts the hashing process starting from an expected hash
# returns the second tuple element that will produce this hash
# based on the fact that the first element produced a given internal state
acc = expected
# only 2 elements
acc -= 2 ^ 2870177450012600261 ^ 3527539
acc %= (2 ** 64)
acc *= 614540362697595703
acc %= (2 ** 64)
acc = (acc & 0x7fffffff) << 33 | (acc >> 31)
acc %= 2 ** 64
acc -= state
acc % (2 ** 64)
acc *= 839798700976720815
return acc % (2 ** 64)
def findCollision(expected):
P = 2305843009213693951
second = P + 1
first = 0
# the 2nd element must be < P otherwise hash(element) != element
while second >= P:
first += 1
second = reverseHash(expected, forwardHash(first))
return (first, second)
from pwn import *
import ast
conn = remote("challenges.france-cybersecurity-challenge.fr", 2103)
conn.recvuntil(b"challenge = ")
challenge = int(conn.recvline().strip())
t = findCollision(challenge)
conn.sendline(str(t[0]).encode())
conn.sendline(str(t[1]).encode())
conn.recvuntil(b"(")
flag = b'('+conn.recvline().strip()
flag = ast.literal_eval(flag.decode())
print(bytes(flag[16:]))
conn.close()
FCSC{658232b18ebebc53c42dd373c6e9bc788f1fd5693cf8a45bcafbff46dae42e24}
Kahl Hash#
Play on HackropoleDifficulty :
Points : 477
Solves : 10
Description :
Do you really know how Python
hashfunction actually works?
The following source code was provided :
#!/usr/bin/env python3.9
try:
flag = tuple(open("flag.txt", "rb").read())
assert len(flag) == 70
challenge = hash(flag)
print(f"{challenge = }")
T = tuple(input(">>> ").encode("ascii"))
if bytes(T).isascii() and hash(T) == challenge:
print(flag)
else:
print("Try harder :-)")
except:
print("Error: please check your input")
This challenge looks suspiciously similar to the previous one but was labeled as harder.

The difference here is that we are working with a tuple of ASCII characters (integers < 128).
During my research for the previous challenge, I found this blog post explaining how to generate collisions for an older version of Python’s hash function using a Meet-in-the-Middle attack.
The idea is as follows:
- Choose a size
sfor the candidate tupleT. There is no restriction in the challenge, so it can be anything, but should be sufficiently large so there are more than enough potential candidates. - For any combination of the last
nelements, recover the internal state that should be produced after having hashed thes-nfirst elements, so the final hash is the expected one. Maintain a list of all those internal states. - For a combination of the first
s-nelements, compute the internal state that will be produced after hashing them. If it is contained in the previous list, a valid tupleThas been found, otherwise try a new combination.
There are 128 possibilities for each element, so I decided to use n=4 which required storing a table of 1284 = 228 elements. I also chose s=16 to give me more flexibility. If you chose s too small and find no candidate T, you’ll have to recompute the first table, as s is involved during the state inversion process.
This attack is more efficient than trying to plainly guess a valid tuple T, instead of having a probability of 2-64 of finding a valid T, you now have a probability of 2-64+28 = 2-36. By spending more ressources on memory, you gain execution time.
I initially thought of implementing this attack in Python, because I could just reuse (after a little adaptation) the code I wrote for the last challenge. But it’s obviously not a good idea, because it would just never find a solution in time.
I wrote it in C.

Here is the abomination :
// gcc -O2 main.c
#include <stdio.h>
unsigned long long rev(const unsigned char * const last) {
/*
inverts the hashing process starting from the expected hash given the 4 last elements.
returns the necessary internal state to produce this hash.
*/
// expected hash
unsigned long long acc = 2077196538114990005ULL;
// hardcoded size : 16
acc -= 16 ^ 2870177450012600261ULL ^ 3527539;
// revert for 4 elements
for (int i=3; i>=0; --i) {
acc *= 614540362697595703ULL;
acc = (acc & 0x7fffffff) << 33 | (acc >> 31);
acc -= last[i] * 14029467366897019727ULL;
}
return acc;
}
unsigned long long thash(const unsigned char * const last) {
// returns the internal state after having hashed 12 tuple element
unsigned long long acc = 2870177450012600261ULL;
for (int i=0; i<12; ++i) {
acc += last[i] * 14029467366897019727ULL;
acc = ((acc << 31) | (acc >> 33));
acc *= 11400714785074694791ULL;
}
return acc;
}
#define N 268435456ULL // 2**28
unsigned long long TABLE[N];
int main(void) {
for (unsigned long long i=0; i<N; ++i) {TABLE[i] = 0;}
unsigned char last[16];
unsigned long long acc;
// Build the table. Not very long
printf("Step1...\n");
for (unsigned char i=0; i<128; ++i) {
last[0] = i;
for (unsigned char j=0; j<128; ++j) {
last[1] = j;
for (unsigned char k=0; k<128; ++k) {
last[2] = k;
for (unsigned char l=0; l<128; ++l) {
last[3] = l;
acc = rev(last);
/*
uncomment the following line when a candidate was found, to print the last 4 elements
This is needed because I can't store the last 4 elements along the internal state.
Need to save space :(
*/
//if (acc == 15893927934471181201ULL) {printf("found one : %02X%02X%02X%02X\n", last[0],last[1],last[2],last[3]);}
// shitty hashmap replacement
TABLE[acc % N] = (acc);
}
}
}
}
// search for T
printf("Step2...\n");
// Because s=16, I will not BF 12 bytes. I fix some to a printable value.
last[6] = 0x41;
last[7] = 0x41;
last[8] = 0x41;
last[9] = 0x41;
last[10] = 0x41;
last[11] = 0x41;
// starting values are adapted for demonstration purposes
for (unsigned char i=2; i<3; ++i) {
last[0] = i;
for (unsigned char j=78; j<79; ++j) {
last[1] = j;
for (unsigned char k=80; k<81; ++k) {
last[2] = k;
for (unsigned char l=0; l<128; ++l) {
last[3] = l;
for (unsigned char a=0; a<128; ++a) {
last[4] = a;
for (unsigned char b=0; b<128; ++b) {
last[5] = b;
acc = thash(last);
// If this is true, we have found a potential candidate
if (TABLE[acc % N] == (acc)) {
printf("Potential candidate: %llu (%02X%02X%02X%02X%02X%02X%02X%02X%02X%02X%02X%02X)\n", acc,last[0],last[1],last[2],last[3],last[4],last[5],last[6],last[7],last[8],last[9],last[10],last[11]);
}
}
}
}
}
}
}
return 0;
}
In less then 3 hours, it found a potential candidate for T :
(0x02, 0x4E, 0x50, 0x18, 0x10, 0x0C, 0x41, 0x41, 0x41, 0x41, 0x41, 0x41, 0x05, 0x33, 0x76, 0x4F)
Converting this to bytes, gives the following solution for the challenge :
b'\x02NP\x18\x10\x0cAAAAAA\x053vO'
FCSC{1d43cd910e5775b80ca7a2c3935fc5c76b207d2bb44a596b474521d776b8e412}
Share It#
Play on HackropoleDifficulty :
Points : 482
Solves : 8
Description :
Scrooge McDuck loves treasure hunts, and he regularly organizes them. He usually buries a real treasure somewhere and invites the hunters to discover the GPS coordinates through various puzzles and riddles to be solved. Scrooge recently shared the coordinates of a buried golden owl with some “trustworthy” friends (who are obviously not supposed to participate to the hunt) so that they are able to recover the treasure in case anything happens to him. Unfortunately, his cupid nephew Donald stole the owl and disappeared with it …
Scrooge swore to never go on that road again! His other passions being programming and mathematics, he decided to implement a tool named
share-itby optimizing the source codesss.cof an obscure cryptographic library calledlibecc. Thanks to his tool, he can share his secret with several persons (including some ushers) by fixing a quorum of minimum shares to be present in order to reveal the secret. This allows Scrooge to be fairly confident that if he shares his secret using the tool with a minimum of persons, it will stay safe: in order to prevent potential malicious collusions of shares holders and force them to be revealed, he neither communicated the quorum size nor the total number of generated shares. Rumours mention around sixty distributed shares though.Evil minded Donald stole a share
share_0.binas well as the tool binaryshare-itfrom an inadvertent cousin. He is convinced that with these sole elements, he can find the secret place where Scrooge recently buried the golden unicorn. Putting faith in your expertise, he promises you half the prize: will you be able to help him?
No source code was provided, only the binary and a single share.

The binary is a stripped 64-bit ELF PIE executable.
The usage is printed when executing it with no options :
# ./share-it
./share-it usage:
gen k n <file name secret of at most 32 bytes>
comb k
We can generate n shares and specify that only k of them are necessary to reveal the secret. For example with n=3, k=2 :
# ./share-it gen 2 3
[+] Generating 3 shares with quorum 2
secret (random): 54e1e402aa454170947e7600721f04e439256725bde149de08849a8ab24cafda
# ls
share-it share_0.bin share_1.bin share_2.bin
# ./share-it comb 2
[+] Combining 2 shares
secret: 54e1e402aa454170947e7600721f04e439256725bde149de08849a8ab24cafda
Judging by the name of the created shares, we are in possession of the first one for the challenge. This will be important later.
In the description we are given the hint, that the code is based on this example from ANSSI’s libecc. This should greatly help identify the functions during the reverse engineering steps and will serve as a reference for pinpointing the modifications.
In IDA, in the main function, with the help of the printed strings, we can identify the 2 core functions :
sss_generate:sub_3CF0sss_combine:sub_3E30
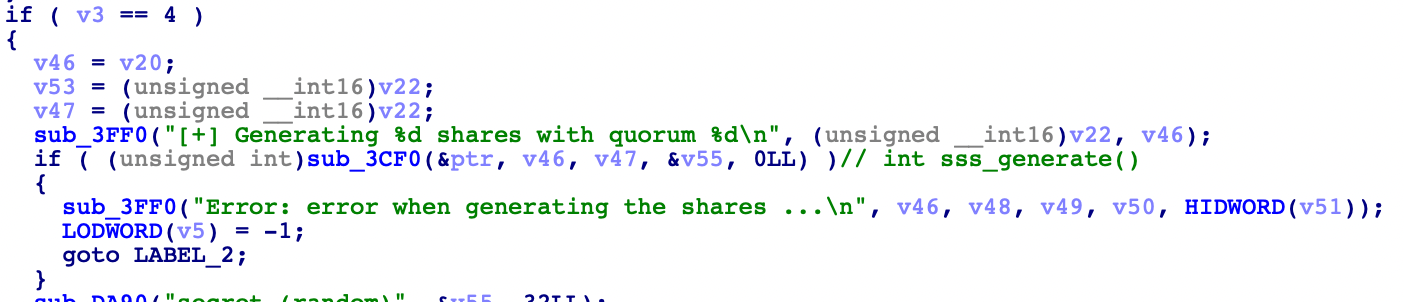
Only the first one is actually interesting in our case. If there has been modifications that would affect the security of the scheme, it was probably done in the generation process.
Now that we have identified a function, we can clone the libecc repository and compile the example program (using the same gcc version). Comparing the disassembled sss_generate function of the example (which isn’t stripped) with our version, allows us to identify even more function names, without too much trouble.
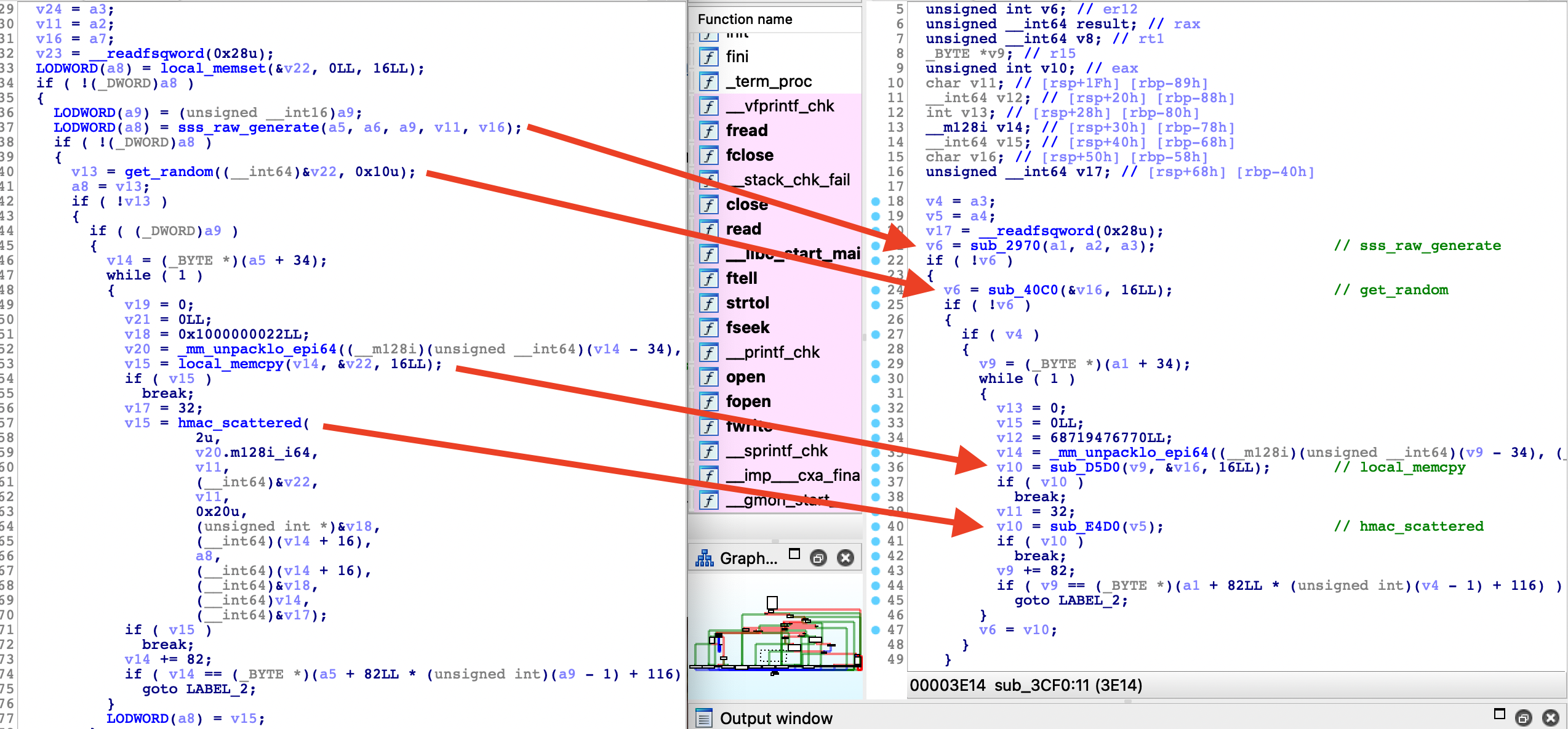
As you can see, the decompiled code is not perfectly identical, but is similar enough to identify functions (in this simple case). It was not that easy for the massive _sss_raw_generate function.
After a lot of renaming, structure definitions, type conversions and comparisons with the original source code, the decompiled code started to look like the example. This is what the final version of the sss_generate function looks like :

Using this methodology, I was able to reverse engineer enough of the generation process to find the differences.
The _sss_derive_seed function has been modified :

Instead of using the seed as a key for the HMAC computation, it uses a newly introduced 2-byte key (passed as a fourth argument) concatenated with the idx parameter, to form a 4-byte value.
This new key is sneakily generated inside the _sss_raw_generate function.
Rewritten in Python, the _sss_derive_seed function is as follows :
import hmac
P = 115792089237316195423570985008687907853269984665640564039457584007908834671663
def _sss_derive_seed(seed, idx, key):
if idx == 0:
return seed
C = bytes([0, idx])
h = hmac.new(key+C, C, "SHA512")
h = int(h.hexdigest(), 16) % P
return (seed*h) % P
We will see later how this will impact the security of the scheme.
The function _sss_derive_seed is used by the _sss_raw_generate function to compute the shares. This part of the code has not been modified and looks like this in Python :
def makeShare(seed, key, base, k):
exp = 1
a0 = _sss_derive_seed(seed, 0, key)
for i in range(1, k):
exp = fp_mul_monty(exp, base)
a = _sss_derive_seed(seed, i, key)
a0 += fp_mul_monty(a, exp)
return a0
More formally : \(S_b = \sum_{i=0}^k a_ib^i\) with \(a_i = sH_i, H_0 = 1\) and b the share’s index starting at a random 2-byte value, s the seed we need to recover, k the number of shares required for the quorum and \(H_i\) the result of the HMAC in the _sss_derive_seed function.
By factoring with the seed, it can be rewritten as \(S_b = s(\sum_{i=0}^k H_ib^i)\) The only real unknown is s. \(S_b\) is our share, b is contained in the share (we have the share numbered 0, so it’s directly b), \(H_i\) is only partially unknown because it depends on a 2-byte key, which can be brute forced, and k can be guessed (<60 from the description). Recovering the seed is thus possible in a reasonable amount of time.
We however have no way to tell if our guesses for k and the HMAC key are correct, besides assuming the seed should respect the flag format.
The file format for the shares is not very complicated :
00000000: 62e2 b89a 285e 5505 b793 969e 235c 0166 b...(^U.....#\.f
00000010: 3279 7029 e7c4 bf17 7917 65ce fce7 3a27 2yp)....y.e...:'
00000020: 450d 5040 6a74 469f 9c58 a0e1 4d37 f026 E.P@jtF..X..M7.&
00000030: 2c95 ecf9 8a54 4a66 8eb3 9025 bae3 42c2 ,....TJf...%..B.
00000040: 5731 a0fd 34bd 1304 e8fc 9204 ccb8 7ad0 W1..4.........z.
00000050: bc6f
The first two bytes represent the base b in big endian, to which was added the share number (0 in our case). The following 32 bytes are \(S_b\) in big endian too. The rest is not relevant for the challenge.
Before implementing the attack, I had rewritten the generation process in Python and wanted to assert it’s indeed doing the same thing as the challenge. The _sss_derive_seed function was OK, but the makeShare function did not work, which was very frustrating as I had a lot of difficulties understanding why. After several hours of debugging with the help of GDB, I finally found the culprit :

How much of a fool was I to even think a simple multiplication function would just return the result of the multiplication ? Take a look at the comments :
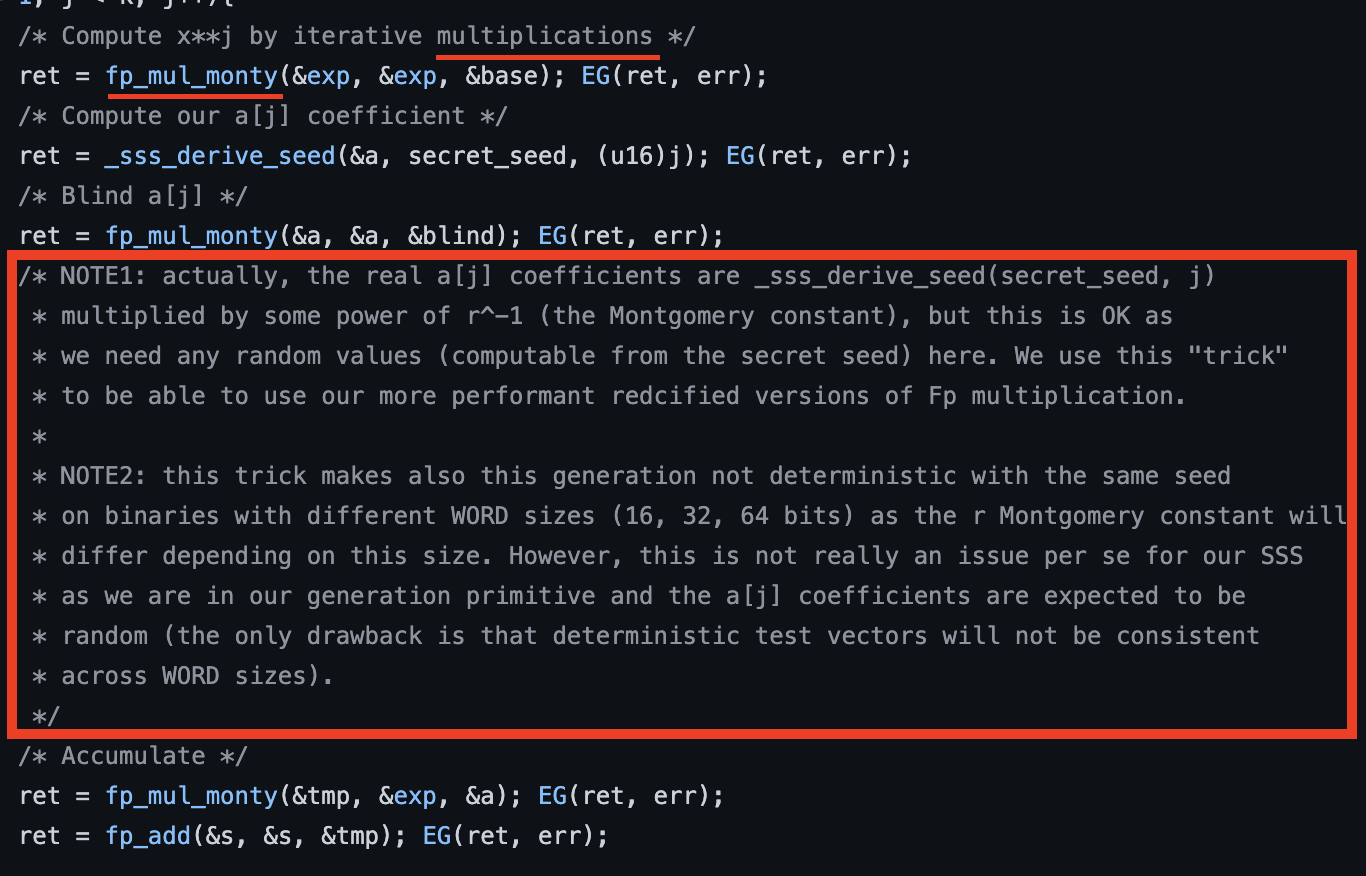
The first one makes you think it’s just a multiplication using a special (optimized ?) algorithm, but the next one actually reveals the odd behavior of this function.
fp_mul(a, b) produces a*b, but fp_mul_monty(a, b) gives a*b*r, and r is some constant dependent on the size of a word on the target machine…
In the case of the challenge this constant is actually :
# fp_mul_monty constant
R = 0xC9BD1905155383999C46C2C295F2B761BCB223FEDC24A059D838091D0868192A
# obtained by modifying sss.c
"""
int main(void)
{
int ret = 0;
fp_ctx ctx;
nn p;
ret = nn_init_from_buf(&p, prime, sizeof(prime)); EG(ret, err);
ret = fp_ctx_init_from_p(&ctx, &p);EG(ret, err);
fp a, b;
ret = fp_init(&a, &ctx);EG(ret, err);
ret = fp_one(&a);EG(ret, err);
ret = fp_init(&b, &ctx);EG(ret, err);
ret = fp_one(&b);EG(ret, err);
ret = fp_mul_monty(&a, &a, &b);EG(ret, err);
unsigned char buff[33];
ret = fp_export_to_buf(buff, 32, &a);EG(ret, err);
for (int i=0; i<32; ++i) {
printf("%02X", buff[i]);
}
printf("\n");
err:
return ret;
}
"""

Now with a fully working Python implementation of the generation process, the attack can be implemented :
import hmac
import gmpy2
P = 115792089237316195423570985008687907853269984665640564039457584007908834671663
# fp_mul_monty constant
R = 0xC9BD1905155383999C46C2C295F2B761BCB223FEDC24A059D838091D0868192A
def fp_mul_monty(a, b):
return (a*b*R) % P
def hi(key, i):
# because the see
if i == 0:
return seed
C = bytes([0, i])
h = hmac.new(key+C, C, "SHA512")
h = int(h.hexdigest(), 16) % P
return h % P
def makeShare(key, base, k):
exp = 1
s = 0
for i in range(1, k):
exp = fp_mul_monty(exp, base)
ai = hi(key, i)
ai = fp_mul_monty(ai, exp)
# because there is another fp_mul_monty during the blinding
# just multiply by R
s += fp_mul_monty(ai, 1)
return s
def recoverSeed(key, base, expected, k):
a = 1
a += makeShare(key, base, k)
# s = s_b / (1 + sum(H_i*b^i))
s = expected * gmpy2.invert(a, P)
s %= P
s = hex(s)[2:].zfill(64)
return bytes.fromhex(s)
expected = 0xb89a285e5505b793969e235c016632797029e7c4bf17791765cefce73a27450d
base = 0x62E2
# tweeked for the demo
for k in range(41, 42):
for keyi in range(65536):
key = keyi.to_bytes(2, 'big')
seed = recoverSeed(key, base, expected, k)
if b'FCSC' in seed:
print(seed)
break
Trying all values of k until 41 did take some time, but in the end the flag appeared.
FCSC{48.8522620000/2.2865220000}
As a fun fact, those coordinates correspond to the location of ANSSI’s office in Paris.
IZNOGOOD#
Play on Hackropole
Difficulty :
Points : 474
Solves : 11
Description :
Your intern does not trust AES and has written his own block cipher. Can you remind him that building custom crypto should be forbidden? :-)
The following source code was provided :
import os
class IZNOGOOD:
def __init__(self, k):
self.k = self._b2n(k)
self.nr = 8
self.S = [12, 5, 6, 11, 9, 0, 10, 13, 3, 14, 15, 8, 4, 7, 1, 2]
self.pi = [
[0x2,0x4,0x3,0xf,0x6,0xa,0x8,0x8,0x8,0x5,0xa,0x3,0x0,0x8,0xd,0x3,
0x1,0x3,0x1,0x9,0x8,0xa,0x2,0xe,0x0,0x3,0x7,0x0,0x7,0x3,0x4,0x4],
[0xa,0x4,0x0,0x9,0x3,0x8,0x2,0x2,0x2,0x9,0x9,0xf,0x3,0x1,0xd,0x0,
0x0,0x8,0x2,0xe,0xf,0xa,0x9,0x8,0xe,0xc,0x4,0xe,0x6,0xc,0x8,0x9],
[0x4,0x5,0x2,0x8,0x2,0x1,0xe,0x6,0x3,0x8,0xd,0x0,0x1,0x3,0x7,0x7,
0xb,0xe,0x5,0x4,0x6,0x6,0xc,0xf,0x3,0x4,0xe,0x9,0x0,0xc,0x6,0xc],
[0xc,0x0,0xa,0xc,0x2,0x9,0xb,0x7,0xc,0x9,0x7,0xc,0x5,0x0,0xd,0xd,
0x3,0xf,0x8,0x4,0xd,0x5,0xb,0x5,0xb,0x5,0x4,0x7,0x0,0x9,0x1,0x7],
[0x9,0x2,0x1,0x6,0xd,0x5,0xd,0x9,0x8,0x9,0x7,0x9,0xf,0xb,0x1,0xb,
0xd,0x1,0x3,0x1,0x0,0xb,0xa,0x6,0x9,0x8,0xd,0xf,0xb,0x5,0xa,0xc],
[0x2,0xf,0xf,0xd,0x7,0x2,0xd,0xb,0xd,0x0,0x1,0xa,0xd,0xf,0xb,0x7,
0xb,0x8,0xe,0x1,0xa,0xf,0xe,0xd,0x6,0xa,0x2,0x6,0x7,0xe,0x9,0x6],
[0xb,0xa,0x7,0xc,0x9,0x0,0x4,0x5,0xf,0x1,0x2,0xc,0x7,0xf,0x9,0x9,
0x2,0x4,0xa,0x1,0x9,0x9,0x4,0x7,0xb,0x3,0x9,0x1,0x6,0xc,0xf,0x7],
[0x0,0x8,0x0,0x1,0xf,0x2,0xe,0x2,0x8,0x5,0x8,0xe,0xf,0xc,0x1,0x6,
0x6,0x3,0x6,0x9,0x2,0x0,0xd,0x8,0x7,0x1,0x5,0x7,0x4,0xe,0x6,0x9],
[0xa,0x4,0x5,0x8,0xf,0xe,0xa,0x3,0xf,0x4,0x9,0x3,0x3,0xd,0x7,0xe,
0x0,0xd,0x9,0x5,0x7,0x4,0x8,0xf,0x7,0x2,0x8,0xe,0xb,0x6,0x5,0x8],
]
self.rk = self.pi
for r in range(self.nr + 1):
for i in range(32):
self.rk[r][i] ^= self.k[i]
def _S(self, s):
return [ self.S[x] for x in s ]
def _P(self, s):
r = []
for j in range(32):
b = 0
for i, x in enumerate(s):
if i == j: continue
b ^= x
r.append(b)
return r
def _addKey(self, a, r):
return [ x ^ y for x, y in zip(a, self.rk[r]) ]
def _n2b(self, v):
L = []
for i in range (0, len(v), 2):
a, b = v[i], v[i + 1]
L.append( b ^ (a << 4) )
return bytes(L)
def _b2n(self, v):
L = []
for x in v:
L.append( (x >> 4) & 0xf )
L.append( x & 0xf )
return L
def encrypt(self, m):
s = self._b2n(m)
for i in range (self.nr - 1):
s = self._addKey(s, i)
s = self._S(s)
s = self._P(s)
s = self._addKey(s, self.nr - 1)
s = self._S(s)
s = self._addKey(s, self.nr)
return self._n2b(s)
KP = 1
flag = open("flag.txt", "rb").read()
k = os.urandom(16)
E = IZNOGOOD(k)
P = [ flag[i:i+16] for i in range(0, len(flag), 16) ]
C = [ E.encrypt(p) for p in P ]
for i in range(len(P)):
if i < KP: print(P[i].hex(), C[i].hex())
else: print("?" * 32, C[i].hex())
#464353437b6661343232653333393434 07b0d32c8a6a25dc782d2ee20acd53f3
#???????????????????????????????? ba596368fc650d3d08ffbfb2bda27f28
#???????????????????????????????? 68be7f31b109babfb667aabb92a119cd
#???????????????????????????????? acf46fe7220bf34cb2fe740c5773b354
This challenge had me puzzled until the end of the CTF.
Here is a list of all the things I tried and didn’t work :
Linear cryptanalysis
Differential Cryptanalysis
Algebraic attacks:
SMT solvers:
- Represent the cipher using z3 (solved 3 rounds in several minutes)
- Meet-in-the-Middle using z3 (solved 4 rounds in 9 seconds, never solved 6)
- Take into consideration the second cipher text bloc and constrain the plaintext to hex (no significant effect)
Polynomial representation of the cipher:
- Gröbner basis reduction (solved only 2 rounds)
- Change S-Box representation to FWBW (no significant effect at best)
- Gröbner sliding (solves 1 round)
- Change term ordering (no effect at best)
- Meet-in-the-Middle + Gröbner basis reduction (no significant effect)
Modify the PRESENT cipher of Cryptapath and use the tool (solved 4 rounds in several minutes)
Other random tests
- Find unmodified key bits through all round keys (there are 2 !)
- Search for related keys 🦘

I had a feeling the vulnerability would come from the permutation layer, because it’s the only thing that was fishy. The round keys are derived using nothing-up-my-sleeve numbers, so there should be no surprise in there.
I gave up after 4 days of struggles.
After having read other participant’s write-up, I was pleased to see I completely missed the vulnerability. At least it wasn’t an implementation/optimization issue on my part.
Millenium#
Play on Hackropole
Difficulty :
Points : 495
Solves : 3
Description :
Our crew of intergalactic rebels is counting on you! Until now, our organization had a secret quantum computer capable of bypassing the cryptographic protections used by the enemy. This allowed us to tamper with our hyperspace travel authorizations.
Unfortunately, the hyperspace travel regulators became suspicious and developed a new authorization method, called “millenium”. This one resists our quantum computer. It is a disaster! All our teams are grounded until further notice.
There is still a new hope, the new signature method has been highly optimized to be efficient and seems to have a parallelepiped anomaly. We need you to find the private key to regain control of the intergalactic network. We have isolated the part we think is vulnerable in the
sign.pyfile, no need to examine thesecure_codefolder. Besides, we managed to get our hands on 300000 signatures and the associated public key, which should be enough to find the enemy’s secret key and sign a travel authorization for one of our ships.
The source code was provided, as well as a set of 300 000 signatures. Only the main file is presented below :
import os
import sys
sys.path.insert(1, './secure_code')
from random import gauss
from Crypto.Hash import SHAKE256
from ntrugen import ntru_solve, gs_norm
from ntt import ntt, intt, div_zq, mul_zq, add_zq
from fft import fft, ifft, sub, neg, add_fft, mul_fft
from common import q
from math import sqrt
def prvkey_gen(n = 128):
while True:
sigma = 1.17 * sqrt(q / (2 * n))
f = [int(gauss(0, sigma)) for _ in range(n)]
g = [int(gauss(0, sigma)) for _ in range(n)]
if gs_norm(f, g, q) > (1.17 ** 2) * q:
continue
f_ntt = ntt(f)
if any((elem == 0) for elem in f_ntt):
continue
try:
F, G = ntru_solve(f, g)
F = [int(coef) for coef in F]
G = [int(coef) for coef in G]
return f, g, F, G
except ValueError:
continue
def pubkey_gen(sk):
f, g, _, _ = sk
return div_zq(g, f)
def hash_to_point(salt, message, n = 128):
k = (1 << 16) // q
shake = SHAKE256.new()
shake.update(salt)
shake.update(message)
hashed = [0 for i in range(n)]
i = 0
j = 0
while i < n:
twobytes = shake.read(2)
elt = (twobytes[0] << 8) + twobytes[1]
if elt < k * q:
hashed[i] = elt % q
i += 1
j += 1
return hashed
# this function has been HIGHLY optimized to be super efficient
def sign(sk, message):
f, g, F, G = sk
B0 = [
[g, neg(f)],
[G, neg(F)],
]
r = os.urandom(40)
point = hash_to_point(r, message)
n = len(point)
B0_fft = [[fft(elt) for elt in row] for row in B0]
[[a, b], [c, d]] = B0_fft
point_fft = fft(point)
t0_fft = [(point_fft[i] * d[i]) / q for i in range(n)]
t1_fft = [(-point_fft[i] * b[i]) / q for i in range(n)]
z0 = [round(elt) for elt in ifft(t0_fft)]
z1 = [round(elt) for elt in ifft(t1_fft)]
z_fft = [fft(z0), fft(z1)]
v0_fft = add_fft(mul_fft(z_fft[0], a), mul_fft(z_fft[1], c))
v1_fft = add_fft(mul_fft(z_fft[0], b), mul_fft(z_fft[1], d))
v0 = [int(round(elt)) for elt in ifft(v0_fft)]
v1 = [int(round(elt)) for elt in ifft(v1_fft)]
s = [sub(point, v0), neg(v1)]
return r, s
def verify(h, message, signature):
r, s = signature
if len(r) != 40:
return False
s0, s1 = s
n = len(s0)
signature_bound = 2 * n * q
hashed = hash_to_point(r, message)
point = add_zq(s0, mul_zq(s1, h))
if point != hashed:
return False
norm_sign = sum(coef ** 2 for coef in s0)
norm_sign += sum(coef ** 2 for coef in s1)
return norm_sign <= signature_bound
def test():
sk = prvkey_gen()
pk = pubkey_gen(sk)
for _ in range(1):
message = os.urandom(32)
sig = sign(sk, message)
print(sig)
assert verify(pk, message, sig)
if __name__ == "__main__":
test()

Conclusion#
As always, the challenges were really good. I found that the difficulty has increased a lot compared to last year.
Even though I did not manage to solve two of the challenges, I’m pretty happy with my performance and learned a lot during the event.

I’m looking forward for next year !