Introduction#
In this post, I’ll present my write-ups for all the challenges listed in the crypto category, ordered by difficulty rating.
The challenges are:
- AdveRSArial Crypto (Baby)
- El Gamal Fait 1/2
- El Gamal Fait 2/2
- The pake is a lie
- AdveRSArial Crypto (Kiddo)
- Broadcastopol
- Salade de fruits
- Share a Saucisse
- Winternitz is coming
- Appellation d’Origine Protégée
- Secret SHenanigans
- Tight Schedule
AdveRSArial Crypto (Baby)#
Play on HackropoleDifficulty :
Points : 258
Solves : 113
Description :
I have perfected my knowledge of RSA, but I’m not sure if my technique to generate the numbers is so smart. Do you confirm?
n = 179770685017248789197537661565815269934203562120851089179122414399064734715990794430000078278988633398024403072323955508476586487162411822366599111412534539430740137196265242371128714558362082882520001747685222655863817125733693411058452743768818267918688593648334613756045157321491607233744902053478170361857
e = 65537
c = 0x000c307feca4371acecab2690800586b967909e12ec3e80184666ca161129f86c6cd87e276127a1f9b672b66ba3d715321b24f7d660a928d829c154dcdc0634b99f51e281c2e138f77a04694ff7aeec25c938cf769fbd7d3f2968f0b96fc5d38a8f742f6a46e70d7eae8280ed61f0328df36497f0cb6251b0e13a2bc5adce6344a
We don’t have the source code to see how the prime numbers where generated, but if we look at the modulus in binary, we see something fishy :
bin(n)
# '0b10000000000000000100000000000000000000000000000000000000000000000010000000000000000000000000000000000000000000000000000000000000000000000000000000000000100000000000010000000000000000100010000100000000100100000000000001000000000000010000000000000000000010000000000010100000000000000100000000000000000001000000000000000110000000000010000000100000000000001000100000000001000000000100000000000001000000000000000000000000100000000000000000000000000000000000010100000010000000000000000000000000000010000000000000000001010000000000000000100000000000000000000000000000000000000000000000010000000000000000000000000000000000000000000000010000000000000000000010000000000000100100000000001000000000000000000001000000100000010000000000000010000000000000000000000000000000000001000000000001000000000000000000000000000000000000100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000010000000000000000000000000000000000000000000000001'
There are a lot less ones then expected. The prime numbers must be very sparse as well. Writing the modulus as a polynomial in base 2 gives us :
x = var('x')
poly = sum(e * x**i for i,e in enumerate(Integer(n).digits(2)))
poly
# x^1024 + x^1007 + x^958 + x^872 + x^859 + x^842 + x^838 + x^833 + x^824 + x^821 + x^807 + x^793 + x^772 + x^760 + x^758 + x^743 + x^723 + x^707 + x^706 + x^694 + x^686 + x^672 + x^668 + x^657 + x^647 + x^633 + x^608 + x^571 + x^569 + x^562 + x^532 + x^513 + x^511 + x^494 + x^445 + x^397 + x^376 + x^362 + x^359 + x^348 + x^327 + x^320 + x^313 + x^298 + x^261 + x^249 + x^212 + x^49 + 1
Factoring polynomials is easier then factoring numbers, so we can try that, just like we did in RSA Destroyer.
poly.factor_list()
# [(x^513 + x^348 + x^327 + x^313 + x^249 + x^212 + 1, 1), (x^511 + x^494 + x^445 + x^359 + x^320 + x^49 + 1, 1)]
We just need to convert both polynomials to numbers and that’s it.
pp, pq = poly.factor_list()
p = pp[0](x=2)
q = pq[0](x=2)
assert p*q == n
FCSC{0224e979da8a6069869ccfc040abb680ffd35e3ba61bcc0e0683662c33fa81c0}
El Gamal Fait 1/2#
Play on HackropoleDifficulty :
Points : 227
Solves : 131
Description :
I was told that you could use RSA to sign messages instead of encrypting them. I tried to do the same with ElGamal. Can you check whether what I’ve done is secure?
The service’s source code was provided :
from Crypto.Random.random import randrange
from Crypto.Util.number import getPrime
def generate(bits):
p = getPrime(bits)
x = randrange(p)
g = randrange(2, p)
y = pow(g,x,p)
return p, g, x, y
def sign(p, g, x, m):
k = randrange(p)
r = pow(g, k, p)
inv_k = pow(k, -1, p - 1)
s = ((m - x * r) * inv_k) % (p - 1)
return r, s
def verify(p, g, y, m, r, s):
if r <= 0 or r >= p - 1 or s < 0 or s >= p - 1:
return False
return pow(g, m, p) == ((pow(y, r, p) * pow(r, s, p)) % p)
print("Public key:")
p, g, x, y = generate(2048)
print(f"{p = }")
print(f"{g = }")
print(f"{y = }")
try:
print("Input a message.")
m = int(input(">>> "))
print("Input a signature. First, input r.")
r = int(input(">>> "))
print("Now, input s.")
s = int(input(">>> "))
if verify(p, g, y, m, r, s):
print("Congratulations! The message and signature match. Here is your flag:")
print(open("flag.txt").read())
else:
print("Better luck next time!")
except:
print("Please check your inputs!")
The goal is to provide a valid ElGamal signature for a message of our choice, under the given public key.
It’s important to note that our message $m$ is not hashed. The ElGamal signature scheme is vulnerable to existential forgeries in this scenario.
Based on the verify function, this is the equation that we must satisfy :
$$ g^m = y^rr^s \mod p $$
Setting $r = gy \mod p$, $s = -r \mod p-1$ and $m = s$ satisfies this equation :
$$ \begin{align*} g^s &= y^{gy}(gy)^s \mod p \\ &= y^{-s}g^sy^s \mod p \\ &= g^s \mod p \end{align*} $$
from pwn import remote
conn = remote("localhost", 4000)
conn.recvuntil(b"p = ")
p = int(conn.recvline())
conn.recvuntil(b"g = ")
g = int(conn.recvline())
conn.recvuntil(b"y = ")
y = int(conn.recvline())
r = g*y % p
s = -r % (p-1)
m = s
conn.sendlineafter(b">>> ", str(m).encode())
conn.sendlineafter(b">>> ", str(r).encode())
conn.sendlineafter(b">>> ", str(s).encode())
print(conn.recvall())
conn.close()
FCSC{9494cb0e1aad8257099a1d1c146b740f01cd9573b26de3370bdd9d09aadcff54}
El Gamal Fait 2/2#
Play on HackropoleDifficulty :
Points : 381
Solves : 50
Description :
I’ve been told that in some cases, my signature service using ElGamal is even easier to attack. Show me how!
The service’s source code was provided :
from Crypto.Random.random import randrange
from Crypto.Util.number import getPrime
def generate(bits):
p = 2
while p % 4 != 1:
p = getPrime(bits)
x = randrange(p)
g = 2
y = pow(g, x, p)
return p, g, x, y
def sign(p, g, x, m):
k = randrange(p)
r = pow(g, k, p)
inv_k = pow(k, -1, p - 1)
s = ((m - x * r) * inv_k) % (p - 1)
return r, s
def verify(p, g, y, m, r, s):
if r <= 0 or r >= p or s < 0 or s >= p - 1:
return False
return pow(g, m, p) == ((pow(y, r, p) * pow(r, s, p)) % p)
print("Public key:")
p, g, x, y = generate(2048)
print(f"{p = }")
print(f"{g = }")
print(f"{y = }")
try:
m = randrange(p)
print(f"Your task is to sign the following message m = {m}")
print("Input a signature. First, input r.")
r = int(input(">>> "))
print("Now, input s.")
s = int(input(">>> "))
if verify(p, g, y, m, r, s):
print("Congratulations! The message and signature match. Here is your flag:")
print(open("flag.txt").read())
else:
print("Better luck next time!")
except:
print("Please check your inputs!")
For this challenge the setup is almost the same, except that we must forge a signature for a specific random message $m$. Furthermore, $g = 2$ and the prime $p$ is chosen so $p \equiv 1 \mod 4$.
This challenge is not as easy as its rating suggests. After some research, I found this paper describing exactly our setup in corollary 2.
If g is smooth and divides p - 1, then it is possible to generate a valid ElGamal signature on an arbitrary value m if $ p \equiv 1 \mod 4$.
Corollary 2 defines $k = (p-3)/2$. Then proceeds to proove that $g^k \equiv (p-1)/g$, which is false :
k=(p-3)//2
pow(g, k, p) == (p-1)/g
# False
pow(g, k, p) - 1 == (p-1)/g
# True
Just ignore this and continue.
Based on theorem 1 and corollary 2, we should take $r = (p-1)/g$ and compute $s = (m - r)k^{-1} \mod p-1$. The couple $(r,s)$ should be a valid signature for the message $m$.
Let’s implement that.
from pwn import remote
conn = remote("localhost", 4000)
conn.recvuntil(b"p = ")
p = int(conn.recvline())
conn.recvuntil(b"g = ")
g = int(conn.recvline())
conn.recvuntil(b"y = ")
y = int(conn.recvline())
conn.recvuntil(b"m = ")
m = int(conn.recvline())
k = (p-3)//2
r = (p-1)//2
s = ((m-r) * pow(k, -1, p-1))%(p-1)
conn.sendlineafter(b">>> ", str(r).encode())
conn.sendlineafter(b">>> ", str(s).encode())
print(conn.recvall())
conn.close()
This does not work everytime. I don’t get it. The theorem says it should work for every $m$ because $p \equiv 1 \mod 4$.

Maybe I’m not smart enough to understand the paper. 🤷♂️
FCSC{095a8d759222a3430328e4a36bc369d739926ce2a836d0e61f67889e80239119}
The pake is a lie#
Play on HackropoleDifficulty :
Points : 442
Solves : 24
Description :
We managed to wiretap our target when it connected to its remote server. Will you manage to find its password? The flag is FCSC{H} where H is the hash of the password using SHA256.
The server’s source code was provided :
import os
import string
from random import randrange
from hashlib import sha256
PASSWORD = os.getenv("PASSWORD", "fake")
class Server:
def __init__(self, password):
# Parameters
self.p = 99126081498110679622117208839946568977975346033127530222404078981480201164078403345496146296949856728918789240336343638617422048283132242454464446291492611584384751501785383357838317732828318093759885347973087134144406693627357857330950504134924555608896346799104280246597972464783116857557440201146239820962614737545356185926303055992966419563962391182588280591946549056511488286585225437441847723071671691983100789423850862625728681245227608953095286385917258671161510940257372122458091056338357381929396029892868891726999599401117716948670950295974901401487901706396092675230119537481992404521806171202857131482218447629266273659693800992655608637431138440796299719773966019160861946691736898018974264372149526585927739463345353811003110493041611686230570445853159167671930184015631656166581888140313132779812582289364648438529584403147703014843916154647757047547530701247017078776589293631650327878203453320557338297607
self.q = 219417094215275962897891584141934286732289959275399446266197828228881499677887
self.gen_p = 5
self.gen_q = 72154714647924720796474763306018150527191193551579074454752226970361323910715225761684479052710319044131664417748053567305559594047843955631623493511776191150761624423057712199333695861546969039213115324133903199540888607688395526099308852693693849968497163766267565896327807964016029443580636143801729508911217765863848341671551118348011046973222684768978887554468357759171837184458551001147236382457538449300832986979798907732863289077628954566687210037771632552199142257829844076857480798150476647417848684957787136264909313143902413998900899314654316452799924876033142970490676851821804729747044276455816438355824263753284809574944174976279150615425997612511094163023294534830728406472125525906164174075985781960904415647895164715282031620157048260175517210288249757399650428148616065918428303867923400176690656556468547499914734843233868999940689417190530787085270228716948016475608585812032578630717685685190825328784
self.key = int(sha256(password.encode()).digest().hex(), 16)
def init_DH(self):
self.x = randrange(2, self.q)
X = pow(self.gen_q, self.x, self.p)
Xenc = self._encrypt(X)
return Xenc
def _encrypt(self, m):
return m * pow(self.gen_p, self.key, self.p) % self.p
def _decrypt(self, c):
return c * pow(self.gen_p, -self.key, self.p) % self.p
def complete_DH(self, Y_enc):
Y = self._decrypt(Y_enc)
self.K = pow(Y, self.x, self.p)
self.H = sha256(hex(self.K).encode() + b"Server").digest().hex()
return self.H
def check_DH(self, your_H):
return your_H == sha256(hex(self.K).encode() + b"Client").digest().hex()
assert len(PASSWORD) == 4
assert all(x in string.ascii_lowercase for x in PASSWORD)
S = Server(PASSWORD)
Xenc = S.init_DH()
print(f"{Xenc = }")
try:
print("Input your part of the Diffie-Hellman exchange (integer mod p):")
Y_enc = int(input(">>> "))
H = S.complete_DH(Y_enc)
print(f"{H = }")
print('Input the hash of the shared key concatenated with "Client" (hex format)')
your_H = input(">>> ")
if S.check_DH(your_H):
print("Connection established!")
else:
print("Not quite, try again!")
except:
print("Check your inputs.")
And this is the result of the wiretaping :
Xenc = 19460524269501469684380940282404035263353475313570685944699777212278714734233974848616532867976938042391556360448138597452928815967385556209404253936404195331278865945748733691583103481233229973739048062149957215958944755071256292474208675643955038432029107148362075643154731697188203476192416818811805475474850424618204910903885276181033693382352648269079678235759177277207911853342711777657979574476592861894959055793978346494827004441820586113252218266204154732012769528643417011794778849554113853620663572084387325155825471739765022830613504350108584120580421755123376416482883250676048630917915780936724250343400455175393922102390667903435317779694694201051038813069086292000645527387556789454121634247313392246822415341019000805020774276218525198099950909055708841086228189494310403615523629305142137297289569411467841488144672894655471512477575751150978532821174700641398949624570034053598900921113884230462963866530
>>> 84670717381205440016719090853798939852418749646038823712435648781665144674461878466063166092569283277546919853772421423008690176544659974816667496981163582048472771734186856375338199938692385892071921329848173035737798082097050940388245739636034935245388068536162882410878110071666242695027971713211776153590965483658618178623976672289798767865497599628578488556347449529427918783922082152119048313627919960326510868635530829264575197739953531608841678502422411582312533043052417916055931979687498721896870961159953728004205770476809412625065667055305692843846613243187997480887311556221895849073881321743490721175815615271924666478464203749498025199664746342454585100519032431215000822959406154079422638289685952728634178556229042892358538313317485004490629892684268877050700293424487323426716589875776900888155996590033379362982943090598235769506118719008120861616330790103010762602452608987506626094830297346246555325568
H = '0589fc1f04fa4393c82a53ec18668897a9e88b6a2fe3de22bb134eb9f7d27a32'
Input the hash of the shared key concatenated with "Client" (hex format)
>>> 3c0416f06455670bb12c8b2865e09874cd4135e26bebf1f744cfc6aed6fcb53e
Connection established!
As the name of the challenge suggests, we are facing a PAKE protocol. Our goal is to recover the 4-character password used during the authentication. As we don’t have access to the server, it cannot be bruteforced online.
Finding the right idea for this challenge was quite tricky actually. There is no obvious issue in the protocol besides the small password space. If only we could find a distinguisher that allowed to test whether a password is correct or not.
Let’s note $k$ the SHA-256 hash of the password, then we have in our possession :
- $\text{Xenc} = G_q^x G_p^k \mod p$, with $x$ the server’s private key.
- $\text{Yenc} = G_q^y G_p^k \mod p$, with $y$ the user’s private key.
For every possible password we can compute $G_p^k$.
To build our distinguisher we have to notice that $p \equiv 1 \mod q$, this means that $q$ is a factor of $p-1$ (the multiplicative order of $G_p$). Could it be that the multiplicative order of $G_q$ is actually $q$ as the name suggests ? It is !
This means that for a correct guess of password, we can compute $\text{Xenc} * G_p^{-k} = G_q^x G_p^kG_p^{-k} = G_q^x \mod p$ and verify that $(G_q^x)^q = 1 \mod p$. If the guess is incorrect, the chances that the order is still $q$ are negligeable. We can also do the same with $\text{Yenc}$.
from sage.all import *
from hashlib import sha256
import string
import itertools
p = 99126081498110679622117208839946568977975346033127530222404078981480201164078403345496146296949856728918789240336343638617422048283132242454464446291492611584384751501785383357838317732828318093759885347973087134144406693627357857330950504134924555608896346799104280246597972464783116857557440201146239820962614737545356185926303055992966419563962391182588280591946549056511488286585225437441847723071671691983100789423850862625728681245227608953095286385917258671161510940257372122458091056338357381929396029892868891726999599401117716948670950295974901401487901706396092675230119537481992404521806171202857131482218447629266273659693800992655608637431138440796299719773966019160861946691736898018974264372149526585927739463345353811003110493041611686230570445853159167671930184015631656166581888140313132779812582289364648438529584403147703014843916154647757047547530701247017078776589293631650327878203453320557338297607
q = 219417094215275962897891584141934286732289959275399446266197828228881499677887
gen_p = Zmod(p)(5)
Xenc = Zmod(p)(19460524269501469684380940282404035263353475313570685944699777212278714734233974848616532867976938042391556360448138597452928815967385556209404253936404195331278865945748733691583103481233229973739048062149957215958944755071256292474208675643955038432029107148362075643154731697188203476192416818811805475474850424618204910903885276181033693382352648269079678235759177277207911853342711777657979574476592861894959055793978346494827004441820586113252218266204154732012769528643417011794778849554113853620663572084387325155825471739765022830613504350108584120580421755123376416482883250676048630917915780936724250343400455175393922102390667903435317779694694201051038813069086292000645527387556789454121634247313392246822415341019000805020774276218525198099950909055708841086228189494310403615523629305142137297289569411467841488144672894655471512477575751150978532821174700641398949624570034053598900921113884230462963866530)
Yenc = Zmod(p)(84670717381205440016719090853798939852418749646038823712435648781665144674461878466063166092569283277546919853772421423008690176544659974816667496981163582048472771734186856375338199938692385892071921329848173035737798082097050940388245739636034935245388068536162882410878110071666242695027971713211776153590965483658618178623976672289798767865497599628578488556347449529427918783922082152119048313627919960326510868635530829264575197739953531608841678502422411582312533043052417916055931979687498721896870961159953728004205770476809412625065667055305692843846613243187997480887311556221895849073881321743490721175815615271924666478464203749498025199664746342454585100519032431215000822959406154079422638289685952728634178556229042892358538313317485004490629892684268877050700293424487323426716589875776900888155996590033379362982943090598235769506118719008120861616330790103010762602452608987506626094830297346246555325568)
for t in itertools.product(string.ascii_lowercase, repeat=4):
password = "".join(t)
key = int(sha256(password.encode()).digest().hex(), 16)
x = gen_p**key
a = Xenc/x
b = Yenc/x
if a**q == b**q == 1:
print(password)
# ltjd
FCSC{f285174468cbce8657478654893edf3b0b3485e5c155db5ee743c4065f57d84c}
AdveRSArial Crypto (Kiddo)#
Play on HackropoleDifficulty :
Points : 413
Solves : 36
Description :
Okay, this time I’m good! I kept my technique to generate sparse numbers for efficiency reasons, but I’m convinced my flag is well protected, right?
n = 32317006071311007300714876688669951960444102669715484116646415746394635540935921521724498858714153019942728273207389351392489359055364847068112159175081645180751388138858639873796530441238955101568733568176426113140426646976937052525918530731769533330028543775101205176486450544323218351858348091394877603920443607214945787590258064663918917740728042628406529049644873974905470262922605695823668958842546472908325174694333334844222696779786423580284135591089906934014814106737656354549850191740172203279085863986305338341130808123659535483768004216490879857791785965848808238698345641038729244197829259714168491081729
e = 65537
c = 0x00bae65fbca88fea74202821d1773fa90e1a6e3532b3e60f1516ad8e04c84c1c42b733206d5b10bfeada9facd35adc426234b31183398adc4d0e842a3a2d09756f9e0bcdfdfe5b553dab4b21ea602eba4dc7db589f69360e1a598048ea0b719e7ab3ca25dec80acdaec582140877da1ce4c912425c43b1e19757309c2383b3b48ebbfcdac5bddfa167bbf1f7a31ec2a7758a52579956600306ca0dab86d5b37d3a7dfc9429a757f978905c01e46bd6d7c32f314a5916107545ad1cb17d76962b4ac11bbb6020a3ff0175d72081cc47cfd486ff05ed8799e2dd0991ce7b4f4ba2f2eae9dbddecc43e9d7a3899f6b493a839d5be7f9fe856fbe238e10047a7ad2945
Just like for the previous RSA challenge, we don’t have the source code to see how the prime numbers where generated. Let’s look at the modulus in binary, again :
bin(n)
# '0b100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000010000000010000000000000000000000000000000000000000000000000000000000000000000010000000000000000000000000000000000000000000000010000000000000000000000000000000000000000000000000000010000000100000000000000000000000000000000000000000000000000000000000000000000100000001000000000000000000000000000000000000000100000000000000000000000000000000000000000001000000000000000000000000000000001000001000011000000000000000000000000000000000000000000000000001000000000000000000000000000000000000000000010001000000000000000000000000000000000010000000010000000000000000000000000000010000110100010100000000000000000000000010000000000000000010000000100000000000000001000010000000000000100010101000000000000000100000100000000000000000000000000000000000000000000000001000000000100000001000000000000000000000000001000000000000000000000000000000000000000000000000000100000001000000000000000000000000100001000000000000000000000000000000001000011000000010000000000000000000000000000100000100000001000000000000000000000000000000000000000000110001001000000001000000000000000000000000011000010000000000000000000000000000000000001000010000000010000000000000000000000000000000010000000000100000000000000000000000000000000000000000100000000000000000000000000000000000001000001000100000000000000000000000000000000000000000000001000000000000000000000000000000000000000000010000000000000000000000000000000100000000000000000000000000000000000000100001100000000000010000000000000000000000000000000000000100000000000000000000000000000000000000000001000100000000000000000000000000000000000000000000000000000000000000000000000000000000000001000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000010000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001'
Like the description says, the same technique seems to be used to generate sparse primes, but as you can imagine, factoring the number as a polynomial in base 2 doesn’t work this time.
This challenge puzzled me for a while, in fact it was one of the last I solved.
I solved it by hand. It was quite laborious and involved some trial and error but I was able to reconstruct the factors progressively. As it’s quite difficult to explain the exact process, and because I haven’t kept much notes of what I did at the time, I will only give a rough idea of how it’s done.

Manual solve
Let’s look at a simple example first :
$$ \begin{align*} p &= & &+ x^{13} & &+ x^5 &+ 1 \\ q &= & & &+ x^{10} & &+ 1 \\ n = pq &= x^{23} &+ x^{15} &+ x^{13} &+ x^{10} &+ x^5 &+ 1 \end{align*} $$
Because $p$ and $q$ are sparse, every term of each of them is also present in $n$. All the other are the possible combinations of terms of $p$ and $q$ : $x^{23} = x^{13}x^{10}$ and $x^{15} = x^{5}x^{10}$.
Because each term only affects the terms greater or equal to them in $n$, we can try to guess the terms of each factor one by one, starting from the lowest one.
If we had to factor the above $n$ using this technique, we would start by setting :
$$ \begin{align*} p &= & & + x^5 &+ 1 \\ q &= & + x^{10} & &+ 1 \\ pq &= x^{15} &+ x^{10} &+ x^5 &+ 1 \end{align*} $$
Because $x^{10}$ and $x^5$ are the two lowest terms, we assumed they were also the two lowest terms of $p$ and $q$. In the resulting product, $x^{15}$ was formed, which is also present in $n$, indicating that our guess is not incorrect.
The next lowest term of $n$ that we are missing is $x^{13}$, so it must be a term of one of the factors as it cannot come from anywhere else. But which one ? Let’s suppose it’s one of $q$ :
$$ \begin{align*} p &= & & & + x^5 &+ 1 \\ q &= & &+x^{13} &+ x^{10} & &+ 1 \\ pq &= x^{18} &+ x^{15} &+ x^{13} &+ x^{10} &+ x^5 &+ 1 \end{align*} $$
The resulting product has the term $x^{18}$, which is not present in $n$, indicating that our guess is incorrect.
This technique can be used to factor $n$ in AdveRSArial Crypto (Baby), but is not sufficient here, otherwise Sage could have factored the polynomial by itself.
The issue is that even if the factors are sparse there is a small chance that they share terms in common. Why is this an issue ? Look at this example :
$$ \begin{align*} p &= & & &+ x^{13} &+ x^5 &+ 1 \\ q &= & & &+ x^{13} & &+ 1 \\ n = pq &= x^{26} &+ x^{18} &+ x^{14} & &+ x^5 &+ 1 \end{align*} $$
As $x^{13}$ apears in both factors, it doesn’t appear in $n$ anymore, instead $x^{14} = 2x^{13}$ is present. Because of this, when applying the above methodology, we run into dead ends, where no choice is correct. We thus have to suppose that one of the terms was common and try to guess which one. This process can be a bit laborious when the polynomials are big, because you might have to rewind several steps of the procedure to find the culprit.
Automatic solve
After the CTF, some people pointed out that they used the same method as in this challenge from GoogleCTF 2020 to factor the modulus.
def order(candidates):
return sorted(candidates, key=lambda pq: bin(pq[0]).count('1') + bin(pq[1]).count('1'))
def recover(n, bits):
candidates = {(0, 0)}
for bit in range(0, bits):
print(bit)
remainder = n % (2 ** (bit + 1))
new_candidates = set()
for potential_p, potential_q in candidates:
# extend by 0 bit and by 1 bit on the left, so candidate 101 -> 0101 and 1101
extended_p = potential_p, (1 << bit) + potential_p
extended_q = potential_q, (1 << bit) + potential_q
for p in extended_p:
for q in extended_q:
if (q, p) not in new_candidates: # p,q and q,p is the same for us
if (p * q) % (2 ** (bit + 1)) == remainder:
new_candidates.add((p, q))
candidates = order(list(new_candidates))[:512]
return candidates
n = 32317006071311007300714876688669951960444102669715484116646415746394635540935921521724498858714153019942728273207389351392489359055364847068112159175081645180751388138858639873796530441238955101568733568176426113140426646976937052525918530731769533330028543775101205176486450544323218351858348091394877603920443607214945787590258064663918917740728042628406529049644873974905470262922605695823668958842546472908325174694333334844222696779786423580284135591089906934014814106737656354549850191740172203279085863986305338341130808123659535483768004216490879857791785965848808238698345641038729244197829259714168491081729
candidates = recover(n, 2048)
for (p, q) in candidates:
if n % p == 0:
print('p', p)
if n % q == 0:
print('q', q)
# p 179769313486231590772930519078902473361797697894230657508039982057879557992101193635465054947335172299030561903611006205008142797276546547887442187227516152781616458268734103382860882441111387866234825627966710855902041331805644963860179151102032696405339203367588103286067326809105174544152798850365136044033
# q 179769313486231590772930519078902473361797697894230657508956426983270756750641042203250349075618771236153547580726603916895893944444813538033577585678487280125223971579128535422517006226698354463073263231618819178369912979902740062477559652404959229975372598382213816270253945896540199960864997790157857882113
FCSC{42d7dc2fb6e5429e4ead6c9c72f561504f514dcfe7de23deb343b43bf0e4120a}
Broadcastopol#
Play on HackropoleDifficulty :
Points : 472
Solves : 12
Description :
The geopolitical scene has taken a turn for the worse for us recently. One of our allies seems to have modified the communications equipment we initially supplied. Indeed, for several days now, our exchanges have been interrupted. However, one of our agents in the field has intercepted one of their broadcasts (
flag.wav.enc). According to our information, it is of tactical importance.One of our cryptographers told us that the encryption algorithm is used in a classic stream cipher mode and that we know that the clear data are WAV files. His team has also managed to obtain a known plaintext (
known.wav/known.wav.enc) for which we know the following:
IV = 0x000dcf18;eck = 0x1119EB502F815EB502F8(eck, Encryption Cipher Key).Furthermore, for the encrypted message
flag.wav.encintercepted, operational analyses indicate that the value of the IV should be0x0026b328.
No source code or binary were provided. Only the three files mentioned in the description.
The first step was guessing the algorithm. Thankfully, we have some clues, the size of the IV is 24 bits and the eck is 80 bits and it’s some kind of stream cipher.
After some time, I found this presentation from Black Hat 2023 that seemed to match.
The algorithm used to encrypt the files is TEA1, which is a stream cipher associated with TETRA, a European standard for public and emergency services. It is part of the TEA suite of encryption algorithms.
As stated here :
The key consists of 80 bits, which is equal to 10 bytes. In the above code, the 10 bytes are processed one at a time, and then shifted into the result (
dwResult) register. However, as thedwResultregister is only 32 bits wide, the first 48 bits are shifted out and the key consists of the last 32 bits only, which is trivially short for a brute-force attack.
The researchers were kind enough to provide an open source implementation of this algorithm.
We just have to adapt the code a little bit to perfom the bruteforce attack and recover the key. Because we know the flag is a WAV file, we have information on the first 4 bytes of the plaintext: “RIFF”, which we will you use to filter out potential key candidates.
#include <inttypes.h>
#include <stdio.h>
#include <stdlib.h>
#include "tea1.h" // Assuming tea1 function is declared and defined in tea1.h
int main() {
uint8_t out[288813];
for (uint32_t key = 0; key < 0xFFFFFFFF; key++) {
tea1(0x0026b328, key, 4, out);
// keystream to have "RIFF" (210, 2, 151, 30)
if (out[0] == 210 && out[1] == 2 && out[2] == 151 && out[3] == 30) {
printf("potential key: %u\n", key);
}
}
return 0;
}
gcc solve.c tea1.c
./a.out
potential key: 202504588
With the key, we can generate the corresponding keystream.
#include <inttypes.h>
#include <stdio.h>
#include <stdlib.h>
#include "tea1.h" // Assuming tea1 function is declared and defined in tea1.h
int main() {
uint8_t out[288813];
uint32_t key = 202504588;
tea1(0x0026b328, key, 288812, out);
// Print the content of the 'out' array in hexadecimal format
// printf("Output in hex: ");
for (int i = 0; i < 288812; i++) {
printf("%02x", out[i]);
}
printf("\n");
return 0;
}
gcc solve.c tea1.c
./a.out > ks.txt
For simplicity, I used Python to decrypt the flag using the generated keystream.
def strxor(a, b):
return bytes([a^b for a,b in zip(a, b)])
flag = open("./flag.wav.enc", "rb").read()
ks = bytes.fromhex(open("ks.txt", "r").read())
open("flag.wav", "wb").write(strxor(flag, ks))
Finally, we can listen for the flag.

The audio quality is so poor, I had to resolve to using a speech-to-text AI to help me understand what the person is saying.
FCSC{bring_me_a_cup_of_tea_one}
Salade de fruits#
Play on HackropoleDifficulty :
Points : 424
Solves : 31
Description :

The challenge is finding the smallest triplet $(x,y,z) \in\mathbb{N}^3$ such that :
$$ x^3+y^3=94z^3 $$
This seemingly simple problem made old nightmares resurface.

At the time of writing this WU, I have forgotten how I got on the right track to find the link between this problem and elliptic curves. It was not easy to find, but here is the question that gave me part of the solution.
The author of the last answer gave a very detailed explanation of the process and also provided a sage implementation. We are interested in the get_selmer_point function :
def get_selmer_point(n, P):
"""Here P = (x, y) is a point on y² = x³ - 432n²"""
x, y = P.xy()
X, Y = (36*n - y)/6/x, (36*n + y)/6/x
denom = gcd(X.denominator(), Y.denominator())
return (X*denom, Y*denom, denom)
This function, given a generator of the curve $E_n: y² = x³ - 432n^2$, returns the smallest triplet $(x,y,z) \in\mathbb{Z}^3$ such that :
$$ x^3+y^3=nz^3 $$
This is almost enough to solve the challenge ($n=94$) but because the triplet is in $\mathbb{Z}^3$ and not $\mathbb{N}^3$, we might get negative values.
E = EllipticCurve([0, -432*(94**2)])
G = E.gen(0)
get_selmer_point(94, G)
# (15642626656646177, -15616184186396177, 590736058375050)
We can find the second smallest solution by using $2G$, and keep increasing the multiple of $G$ until we find a solution in $\mathbb{N}^3$.
from hashlib import sha256
from sage.all import *
E = EllipticCurve([0, -432*(94**2)])
G = E.gen(0)
for i in range(1, 100):
try:
x,y,z = get_selmer_point(94, G*i)
if x**3 + y**3 == 94*z**3:
if x > 0 and y > 0 and z > 0:
print(x,y,z)
h = sha256(str(z).encode()).hexdigest()
print(f"FCSC{{{h}}}")
exit(1)
except ArithmeticError:
pass
FCSC{2c69e5056f2a80af36c0880a2395472e51b448730a1c5c06b2b0d8e0a3b466b6}
Share a Saucisse#
Play on HackropoleDifficulty :
Points : 434
Solves : 27
Description :
It’s your friend Adi’s birthday. You wanted to prank him at his birthday party by hiding a hidden message in each of the 17 sausages prepared for the guests. Unfortunately, the barbecue caught fire and Adi could only save 16 out of the 17 sausages. Can he still figure it out?
The following source code was provided :
import os
import json
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
class SSS:
def __init__(self, secret, k):
self.p = 931620319462745440509259849070939082848977
self.k = k
self.polynomial = [ int.from_bytes(secret) ]
for _ in range(k):
self.polynomial.append(int.from_bytes(os.urandom(16)))
self.index = int.from_bytes(b"FCSC2024")
def eval_poly(self,x):
return sum(self.polynomial[j] * (x ** j) for j in range(self.k + 1)) % self.p
def generate_share(self):
self.index = self.index + 1
return self.index, self.eval_poly(self.index)
if __name__ == "__main__":
key = os.urandom(16)
iv = os.urandom(16)
flag = pad(open("flag.txt", "rb").read().strip(), AES.block_size)
E = AES.new(key, mode = AES.MODE_CBC, iv = iv)
flag_enc = E.encrypt(flag)
k = 16
s = SSS(key, k)
shares = [ s.generate_share() for _ in range(k) ]
data = {
"iv": iv.hex(),
"flag_enc": flag_enc.hex(),
"shares": shares,
}
print(json.dumps(data, indent = 4))
As well as the following data :
{
"iv": "1f07fa2c52e76d19abe62383f3f4103e",
"flag_enc": "cab6478f8e16df758c3dc4f341ead6080f115bea34a0c2c7d2932f6422313696f13e446a1fcab0c6fb8a94fe26d4152232b1fb3feb89f3bd3e5b7af28302721a5a6e92b4110f7c7277f25250230d3803",
"shares": [
[
5062981954164503093,
295592704039076973906624580976591996843865
],
[
5062981954164503094,
209004930188439163881955907953368403287940
],
...
]
}
The code is an implementation of Shamir’s secret sharing (SSS).
SSS works by generating a random polynomial $f(x)$ on $GF(p)$ with $k$ terms :
$$ f(x) = a_0 + a_1x + a_2x^2 + a_3x^3 + … + a_{k-1}x^{k-1} $$
$a_0$ is the secret and elements $a_1$ to $a_{k-1}$ are randomly sampled from $GF(p)$. Each share correspond to a tuple $(i, f(i))$. To recover the secret, $k$ or more shares are required.
We are in possession of 16 shares, but in order to recover the secret, a quorum of 17 shares is required. Luckily for us, there is a flaw in the implementation.
Instead of generating the coefficients $a_i$ of the polynomial uniformely between $[0, p-1]$, they are sampled from $[0, 2^{128}[$. Because of this, they are (with very high probability) significantly smaller than a random element of $GF(p)$, because $p$ is 140 bits long.

From the knowledge of the 16 shares, we can write a system of equation in matrix form :
$$ S = \begin{bmatrix} 1 & 1 & \cdots & 1 \\ x_1 & x_2 & \cdots & x_{16} \\ x_1^2 & x_2^2 & \cdots & x_{16}^2 \\ \vdots & \vdots & \ddots & \vdots \\ x_1^{16} & x_2^{16} & \cdots & x_{16}^{16} \\ -f(x_1) & -f(x_2) & \cdots & -f(x_{16}) \end{bmatrix} $$
Notice that the linear combination $\mathbf{t} = (a_0, a_1, a_2, \cdots, a_{16}, 1)$ produces the zero vector $\mathbf{t}S = (0, 0, 0, \cdots, 0)$ modulo $p$. Because $\mathbf{t}$ is a short vector of this lattice, we can try to recover it using lattice reduction thanks to the LLL algorithm. But to make $\mathbf{t}$ appear after the reduction, we have to construct a more elaborate matrix :
$$ M = \begin{bmatrix} I_{18} & cS \\ 0 & cpI_{16} \end{bmatrix} $$
$I_{18}$ is the 18*18 identity matrix with a twist. The element on the last column and last row is not 1, but a special sentinel value $u$. I’ll explain its use later. The role of this matrix is to reflect the vector $\mathbf{t}$ into the reduced basis.
$$ I_{18} = \begin{bmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & u \end{bmatrix} $$
$cS$ is the matrix $S$ multiplied by a coefficient $c$. I’ll explain why later. Notice that the introduction of this coefficient does not affect the result of the system of equations.
$cpI_{16}$ is the 16*16 identity matrix, multiplied by $cp$. Its use is to convert the previous system of linear equations into a modular system of equation by adding and extra term $k_icp$ to each share’s equation.
$$ cpI_{16} = \begin{bmatrix} cp & 0 & \cdots & 0 \\ 0 & cp & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & cp \end{bmatrix} $$
Here is the expanded 34*34 matrix $M$ to better visualize what’s happening :
$$ M = \begin{bmatrix} 1 & 0 & \cdots & 0 & 0 & c & c & \cdots & c \\ 0 & 1 & \cdots & 0 & 0 & cx_1 & cx_2 & \cdots & cx_{16} \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 & 0 & cx_1^{16} & cx_2^{16} & \cdots & cx_{16}^{16} \\ 0 & 0 & \cdots & 0 & u & -cf(x_1) & -cf(x_2) & \cdots & -cf(x_{16}) \\ 0 & 0 & \cdots & 0 & 0 & cp & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 & 0 & 0 & cp & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & cp \end{bmatrix} $$
Notice that the linear combination $\mathbf{v} = (a_0, a_1, a_2, \cdots, a_{16}, 1, k_1, k_2, \cdots, k_{16})$ produces the short vector $\mathbf{v}M = (a_0, a_1, a_2, \cdots, a_{16}, u, 0, 0, 0, \cdots, 0)$. It is likely that this vector can be found among the basis vectors of an LLL-reduced basis, if the sentinel value $u$ and the coefficient $c$ are chosen accordingly.
The coefficient $c$ must be chosen to ensure our target vector is smaller than any vector of the non-reduced basis $M$. Without ponderation ($c=1$), the vector formed by the first row of $M$ is clearly smaller than $\mathbf{v}M$. Choosing $c = 2^{140}$ makes this vector about the same size as an average vector, making it disappear from the LLL-reduced basis.
This trick alone is not enough to recover our target vector. It seems as if the reduced-basis has several shorter vectors that satisfy the constraints of our system. Using the sentinel value $u$ we can impose another constraint on the system. We want to force the use of the 17th row only one time in the resulting linear combination ($\mathbf{v}[17] = 1$). To do so, we can set $u = 2^{128}$, because this is about the same size as the coefficients $a_i$ of our target vector. It should be big enough to prevent the row vector from being taken multiple times by LLL (it would be too big to apear in the reduced basis) and it should be small enough to not make our target vector too big.
Lastly, we can distinguish a potential candidate vector in the LLL-reduced basis if we see the sentinel value $u$ at the 17th position, followed by 16 zeros.
from sage.all import *
from Crypto.Cipher import AES
from Crypto.Util.number import long_to_bytes
shares=[
[
5062981954164503093,
295592704039076973906624580976591996843865
],
# ...
]
p=931620319462745440509259849070939082848977
n = len(shares)
c = 2**140
u = 2**128
Pn = Matrix.identity(n) * p * c
Zn = Matrix.zero(n, n+2)
In2 = Matrix.identity(n+2)
In2[-1, -1] = u
Sn = Matrix([[pow(e[0],i,p) for e in shares] for i in range(17)]) * c
Sn = Sn.stack(vector([-e[1] * c for e in shares]))
M1 = In2.augment(Sn)
M2 = Zn.augment(Pn)
M = M1.stack(M2)
L = M.LLL()
for e in L:
if e[17] == u and all(x == 0 for x in e[18:]):
print(e)
try:
E = AES.new(long_to_bytes(e[0], 16), mode = AES.MODE_CBC, iv = bytes.fromhex("1f07fa2c52e76d19abe62383f3f4103e"))
print(E.decrypt(bytes.fromhex("cab6478f8e16df758c3dc4f341ead6080f115bea34a0c2c7d2932f6422313696f13e446a1fcab0c6fb8a94fe26d4152232b1fb3feb89f3bd3e5b7af28302721a5a6e92b4110f7c7277f25250230d3803")))
except:
pass
FCSC{67ff5c80109bf5fb1340d1d3da6d94c2fa6c22523e49de2bd3b25df02580d257}
Winternitz is coming#
Play on HackropoleDifficulty :
Points : 456
Solves : 18
Description :
I introduce you to the most groundbreaking and never seen before one time signature! And let me be very clear, I’ve taken great care to sign only one message. So believe me when I say there’s absolutely nothing to worry about folks. Absolutely nothing!
The service’s source code was provided :
import os
from ast import literal_eval
from hashlib import sha256
class WiC:
def __init__(self, W = 257, msglen = 20, siglen = 40):
# Parameters
self.W = W
self.msglen = msglen
self.siglen = siglen
self.n1 = self.siglen // 256 + 1
self.n2 = self.W // 256 + 1
# Evaluation points chosen uniformly at random
self.Support = [
8, 17, 26, 32, 52, 53, 57, 58,
59, 63, 64, 66, 67, 71, 73, 76,
79, 81, 111, 115, 132, 135, 141, 144,
151, 157, 170, 176, 191, 192, 200, 201,
202, 207, 216, 224, 228, 237, 241, 252,
]
# Run key generation
self._keygen()
def _keygen(self):
sk_seed = os.urandom(16)
mask_seed = os.urandom(16)
SK = [
sha256(sk_seed + i.to_bytes(self.n1)).digest()
for i in range(self.siglen)
]
PK = SK.copy()
for i in range(self.siglen):
for j in range(1, self.W):
PK[i] = self._H(PK[i], mask_seed, i, j)
self.sk = (mask_seed, sk_seed)
self.pk = (mask_seed, PK)
def _byte_xor(self, b1, b2):
assert len(b1) == len(b2), "Error: byte strings of different length."
return bytes([x ^ y for x, y in zip(b1, b2)])
def _encoding(self, msg):
w = [0] * len(self.Support)
for i in range(len(self.Support)):
for j in range(len(msg)):
# Constant coefficient is zero
w[i] += msg[j] * self.Support[i] ** (j + 1)
w[i] %= self.W
return w
def _H(self, s, m, i, j):
return sha256(
self._byte_xor(
s,
sha256(
m + i.to_bytes(self.n1) + j.to_bytes(self.n2)
).digest()
)
).digest()
def sign(self, message):
if len(message) > self.msglen:
print("Error: message too long.")
return None
mask_seed, sk_seed = self.sk
w = self._encoding(message)
S = [
sha256(sk_seed + i.to_bytes(self.n1)).digest()
for i in range(self.siglen)
]
for i in range(self.siglen):
for j in range(1, w[i] + 1):
S[i] = self._H(S[i], mask_seed, i, j)
return [s.hex() for s in S]
# message is a list of bytes
def verif(self, message, signature):
if len(message) > self.msglen:
print("Error: message too long.")
return None
mask_seed, PK = self.pk
w = self._encoding(message)
for i in range(self.siglen):
for j in range(w[i] + 1, self.W):
signature[i] = self._H(signature[i], mask_seed, i, j)
return all(s == pk for s, pk in zip(signature, PK))
S = WiC()
pk = (
S.pk[0].hex(),
[ pk.hex() for pk in S.pk[1] ]
)
message = b"WINTERNITZ IS COMING"
signature = S.sign(message)
print (f"{message = }")
print (f"{signature = }")
print (f"{pk = }")
try:
print("Input your message (hex format):")
your_message = bytes.fromhex(input(">>> "))
print("Input your signature (list of hex strings):")
your_signature = literal_eval(input(">>> "))
your_signature = [bytes.fromhex(s) for s in your_signature]
assert message != your_message
assert len(your_message) == 20
assert len(your_signature) == 40
if S.verif(your_message, your_signature):
print("Congratulations! Here is your flag:")
print(open("flag.txt").read())
else:
print("Not quite, try again!")
except:
print("Please check your inputs.")
The WiC class is an implementation of Winternitz One-Time Signatures (WOTS).
We are given a signature for a fixed message and have to forge a new valid signature for a message of our choice.
Let’s start with a quick overview of what the server is doing, without going into the details.
This signature scheme works by first generating a private key $X$, which is an array of 40 256-bit random values. The public key $P$ is also an array of 40 elements, computed by iteratively hashing each element of the private key 256 times.
To generate a signature $S$, a message $m$ is encoded as an array of 40 elements $M$ by the WiC._encoding function. We’ll look at this one later.
After encoding, each element of the private key is iteratively hashed $M_i$ times, to produce the signature (array of 40 elements).
The signature verification is similar, the encoded message array is iteratively hashed element-wise $256-M_i$ times and the result is compared to the public key.
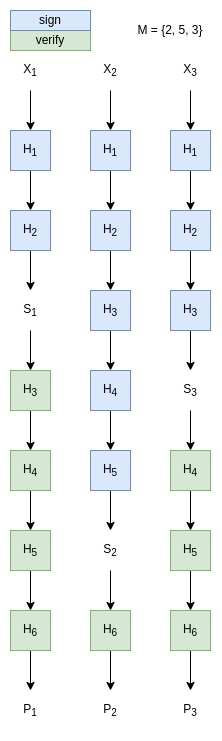
It is clear that if we manage to find a new message $m’$ whose elements after encoding are all bigger then or equal to those of $M$, we can forge a new signature by simply continuing the hash chain.
It’s time to look into the message encoding in more details.
class WiC:
def __init__(self, W = 257, msglen = 20, siglen = 40):
# Parameters
self.W = W
# ...
# Evaluation points chosen uniformly at random
self.Support = [
8, 17, 26, 32, 52, 53, 57, 58,
59, 63, 64, 66, 67, 71, 73, 76,
79, 81, 111, 115, 132, 135, 141, 144,
151, 157, 170, 176, 191, 192, 200, 201,
202, 207, 216, 224, 228, 237, 241, 252,
]
def _encoding(self, msg):
w = [0] * len(self.Support)
for i in range(len(self.Support)):
for j in range(len(msg)):
# Constant coefficient is zero
w[i] += msg[j] * self.Support[i] ** (j + 1)
w[i] %= self.W
return w
Messages must have a length of 20 characters at most.
Let’s rename the variable Support to $a$. The elements of the encoded message $M$ are computed as such :
$$ \begin{align*} M_0 &= m_0a_0^1 + m_1a_0^2 + \cdots + m_{19}a_0^{20} \mod 257\\ M_1 &= m_0a_1^1 + m_1a_1^2 + \cdots + m_{19}a_1^{20} \mod 257\\ \vdots \\ M_{39} &= m_0a_{39}^1 + m_1a_{39}^2 + \cdots + m_{19}a_{39}^{20} \mod 257\\ \end{align*} $$
Or rewritten in Matrix form :
$$ M = Am = \begin{bmatrix} a_0^1 & a_0^2 & \cdots & a_0^{20} \\ a_1^1 & a_1^2 & \cdots & a_1^{20} \\ \vdots & \vdots & \ddots & \vdots \\ a_{39}^1 & a_{39}^2 & \cdots & a_{39}^{20} \end{bmatrix} \begin{bmatrix} m_0 \\ m_1 \\ \vdots \\ m_{19} \end{bmatrix} \mod 257 $$
As $A$ is not square, it’s not inversible. But we can still recompute $m$ from $M$ by solving the linear system of equations.
A simple idea that comes to mind to try and solve the challenge is just to randomly increment every element of $M$ and try to solve the system of equations to recover a message for which we can compute a signature :
Support = [
8, 17, 26, 32, 52, 53, 57, 58,
59, 63, 64, 66, 67, 71, 73, 76,
79, 81, 111, 115, 132, 135, 141, 144,
151, 157, 170, 176, 191, 192, 200, 201,
202, 207, 216, 224, 228, 237, 241, 252,
]
A = Matrix(Zmod(257), [
[pow(a, i, 257) for i in range(1, 21)]
for a in Support
])
message = b'WINTERNITZ IS COMING'
M = A * vector(message.ljust(20, b'\x00'))
# (131, 11, 208, 118, 239, 239, 179, 68, 14, 202, 176, 127, 207, 180, 240, 189, 209, 243, 37, 212, 241, 50, 177, 250, 207, 234, 91, 239, 125, 235, 165, 139, 226, 65, 148, 235, 208, 75, 243, 27)
import random
def randM(M):
N = M[::]
for i,e in enumerate(M):
N[i] += random.randrange(0, 256-N[i])
return N
while True:
N = randM(M)
try:
m = bytes(A.solve_right(vector(N)))
print(m)
break
except ValueError:
pass
But of course, this simple bruteforce approach doesn’t work.

A better solution is to rely on lattices again. If $A$ is the basis of a lattice, then $M$ is a vector of that lattice, as it’s the result of a linear combination of the basis vectors ($M = Am$). We are searching for another lattice vector that is close to $M$ and that satisfies our constraits. This is a special case of the CVP.
Let’s consider the lattice spanned by the rows of the following basis:
$$ K = \begin{bmatrix} a_0 & a_1 & \cdots & a_{39} & 0 \\ a_0^2 & a_1^2 & \cdots & a_{39}^2 & 0 \\ \vdots & \vdots & \ddots & \vdots \\ a_0^{20} & a_1^{20} & \cdots & a_{39}^{20} & 0 \\ -T_0 & -T_1 & \cdots & -T_{39} & 1 \\ 257 & 0 & \cdots & 0 & 0 \\ 0 & 257 & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 257 & 0 \end{bmatrix} $$
$T$ is a target vector for which we want to find the closest vector that lies on the lattice. If $T$ is close to a lattice vector $V$, applying LLL on this basis would likely yield a reduced basis containing the vector $T-V$ (or $-(T-V)$, hence the use of the last column to determine the sign), as it would be small. Other vectors of the resulting basis could be used to compute a lattice vector close to T, but not necessarily the closest.
How do we choose $T$ ? Choosing $T = M$ is an improvement to our bruteforce search, as the LLL-reduced basis would allow us to compute several candidate vectors on the lattice (for which a solution to the system of equations exists), close to $M$. This is however still not very usefull because the vectors likely won’t satisfy the needed constrainsts.
To maximize our chances of finding a lattice vector $V$ with $M_i \le V_i \le 256, \forall i \in [0,39]$, we’ll choose $T_i = \frac{M_i + 256}{2}, \forall i \in [0,39]$.
from sage.all import *
Support = [
8, 17, 26, 32, 52, 53, 57, 58,
59, 63, 64, 66, 67, 71, 73, 76,
79, 81, 111, 115, 132, 135, 141, 144,
151, 157, 170, 176, 191, 192, 200, 201,
202, 207, 216, 224, 228, 237, 241, 252,
]
A = Matrix(Zmod(257), [
[pow(a, i, 257) for i in range(1, 21)]
for a in Support
])
message = b'WINTERNITZ IS COMING'
M = A * vector(message.ljust(20, b'\x00'))
M = M.change_ring(ZZ)
# target a vector in the middle of upper and lower bounds
target = vector([(l + u) // 2 for u, l in zip([256]*40, M)])
P = matrix.identity(40) * 257
K = A.T.stack(-target).change_ring(ZZ)
K = K.stack(P)
u = 1
z = matrix.zero(61, 1)
z[20] = u
K = K.augment(z)
L = K.LLL()
for e in L:
try:
if e[-1] == u:
v = target + e[:-1]
elif e[-1] == -u:
v = target - e[:-1]
else:
continue
m = bytes(A.solve_right(v))
# check M' satisfies constraints
if all(a>=b and a<257 for a,b in zip(v, M)):
print(m)
# b'\x8f\x0e@;\n\x0b\x96p\r\xb0H\xe5\xecN\x01\xa8c4\xbe\x87'
except ValueError:
pass
With a valid new message $m’$ all that’s left to do is advance the hash chain to compute the signature.
from pwn import *
from ast import literal_eval
from hashlib import sha256
class WiC:
# ...
S = WiC()
def encode(msg):
w = [0] * 40
for i in range(40):
for j in range(len(msg)): # 20
# Constant coefficient is zero
w[i] += msg[j] * S.Support[i] ** (j + 1)
w[i] %= 257
return w
def sign(pk, sig, message):
mask_seed = bytes.fromhex(pk[0])
w = encode(message)
w_ = encode(b'WINTERNITZ IS COMING')
s = [
bytes.fromhex(e)
for e in sig
]
for i in range(40):
for j in range(w_[i]+1, w[i] + 1):
s[i] = S._H(s[i], mask_seed, i, j)
return [e.hex() for e in s]
conn = remote("localhost", 4000)
conn.recvuntil(b"signature = ")
signature = literal_eval(conn.recvline().strip().decode())
conn.recvuntil(b"pk = ")
pk = literal_eval(conn.recvline().strip().decode())
my = b'\x8f\x0e@;\n\x0b\x96p\r\xb0H\xe5\xecN\x01\xa8c4\xbe\x87'
mysig = sign(pk, signature, my)
conn.sendline(my.hex().encode())
conn.sendline(str(mysig).encode())
conn.interactive()
FCSC{e2987e3e48e51343df63218484d5e760faf5cf15c9f01a8649a483a91c31ce11}
Appellation d’Origine Protégée#
Play on HackropoleDifficulty :
Points : 482
Solves : 8
Description :
A consumer product labeling company has decided to certify its products using highly innovative NFTs. The company didn’t want to do things halfway, so they created their own blockchain.
Your friend, a sparkling wine producer, wants to take advantage of this to upgrade. With his computer skills, he managed to find a “pseudo-random” permutation used in the blockchain, and needs to solve the CICO problem to finally be able to sell champagne.
Can you help him?
The service’s source code was provided :
from hashlib import sha256
class AOP:
def __init__(self, s = 1):
self.p = 18446744073709551557 # p - 1 not a multiple of 3
self.t = 5
self.r = 9
self.RC = [
[ int.from_bytes(sha256(b"FCSC2024#" + str(self.t*j + i).encode()).digest()) % self.p for i in range(self.t) ]
for j in range(self.r)
]
self.M = [
[ pow(i, j, self.p) for i in range(1, self.t + 1) ]
for j in range(self.t)
]
def R(self, r):
# self.S <- self.S * M
s = [ 0 ] * self.t
for j in range(self.t):
acc = 0
for i in range(self.t):
s[j] += self.M[i][j] * self.S[i]
s[j] %= self.p
self.S = s[:]
# self.S <- self.S + RC[i]
for j in range(self.t):
self.S[j] += self.RC[r][j]
# self.S <- self.S ** e
e = pow(3, -r, self.p - 1)
self.S[0] = pow(self.S[0], e, self.p)
def __call__(self, L):
assert len(L) == self.t, f"Error: input must be a list of {self.t} elements."
assert all(x in range(0, self.p) for x in L), f"Error: elements must be in [0..{self.p - 1}]."
self.S = L[:]
for i in range(self.r):
self.R(i)
return self.S
if __name__ == "__main__":
try:
aop = AOP()
print("Input your values as a comma-separated list: ")
X = input(">>> ").split(",")
X = [ int(x) for x in X ]
Y = aop(X)
if X[0] == 0 and Y[0] == 0:
flag = open("flag.txt").read()
print(flag)
else:
print("Nope!")
except:
print("Please check your inputs.")
exit(1)
This challenge expects us to find a tuple X of 5 elements, with X[0] == 0, that once fed to the AOP class, produces another tuple Y with Y[0] == 0.
For me, this was the hardest challenge of the category and it was the last one I solved. Funnily, it was also the last one I wrote in this post. Partly because I can’t comprehend what I did in any of my 5 “solve” scripts, but also because I don’t remember the numerous rabbit holes I went into. All I remember is that solving this challenge was a real pain and trying to explain how I did it would require doing it again…

Let’s rewrite the transformation performed by the AOP class in Sage for more readability :
from hashlib import sha256
from sage.all import *
# Constants
p = 18446744073709551557
t = 5
r = 9
RC = Matrix(Zmod(p), [
[ int.from_bytes(sha256(b"FCSC2024#" + str(t*j + i).encode()).digest()) for i in range(t) ]
for j in range(r)
])
M = Matrix(Zmod(p), [
[ pow(i, j, p) for i in range(1, t + 1) ]
for j in range(t)
])
E = [pow(3, -i, p - 1) for i in range(r)]
# round, v is a vector of 5 elements, i is the round index
def R(i, v):
v *= M
v += RC[i]
v[0] = v[0]**E[i]
return v
def enc(L):
S = L[:]
for i in range(r):
S = R(i, S)
return S
I’m not sure what this class implements. It’s not a cipher as there is no key and it’s not a hash function as the transformation is inversible.
Regardless, I’ll call enc the original transformation and dec the inverse :
M_ = M.inverse()
E_ = [pow(3, i, p - 1) for i in range(r)]
def R_(i, v):
t = v[::]
t[0] = t[0]**E_[i]
t -= RC[i]
t *= M_
return t
def dec(L):
S = L[:]
for i in range(r-1, -1, -1):
S = R_(i, S)
return S
As the transformation was only using algebraic operations, I naturally tried algebraic attacks. I spent days trying to solve the challenge by representing the AOP transformation using polynomials and doing Gröbner basis reductions. I’ll spare you the implementation details of my failed attempts :
- Gröbner basis reduction on
dec(solved only 5 rounds) - Gröbner sliding (solves 5 round)
- Change term ordering (no effect at best)
- Meet-in-the-Middle + Gröbner basis reduction (no significant effect)
As nothing was close to solving the 9 rounds of AOP, I started to look for papers to give me clues on how to approach the problem more efficiently.
The name AOP actually stands for Arithmetization-Oriented Primitives. I found that out thanks to this paper while searching what the CICO problem was and its link with blockchain. This paper also gives the solution to the challenge in chapter 4.2 (case $t \geq 3$). Let’s break it down.
The trick presented in the paper allows to skip a round. The idea is to reduce the number of variables after the first round, to a single one: $X$. This way, the resulting output (we are only interested in the first element) will be expressed as a polynomial $f(X)$. Because we want $f(X) = 0$, a solution to the CICO problem can be computed by searching for the roots of $f$.
The degree of the resulting polynomial for AOP will be too big if working in the “encryption” direction like it’s requested by the challenge, because the exponents in E are very big. Instead, we can work in the other direction.
To summarize, we are looking for an output vector $O$, with $O_0 = 0$, such that after applying $R_8^{-1}$ (the inverse round function R_) it becomes a vector $V = (a, bX, cX, dX, eX)$ with only one unknown $X$. The elements $a, b, c, d, e$ are constants we will choose carefully later on. Propagating this vector through the rest of the rounds will produce an input vector $I$ composed of polynomials for which we will have to find the roots of $I_0 = f(X) = 0$.
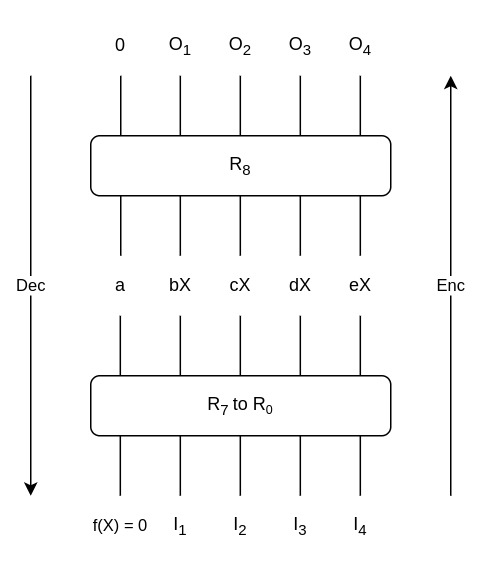
Reducing the number of variables
Let’s start by determining $O$ from the desired vector $V$ :
from aop import *
# Define the variables
P = PolynomialRing(Zmod(p), names="a,b,c,d,e,X")
a, b, c, d, e, X = P.gens()
# We are looking for a vector of this form after R_(8)
V = vector([a, b*X, c*X, d*X, e*X])
# To construct the required output vector O we compute R(8, v)
# because O[0] == 0, we can ignore this step that would be impossible to compute symbolicly: v[0] = v[0]**E[i]
O = (V*M)+RC[8]
print(O[0])
# b*X + c*X + d*X + e*X + a + 18149433503814401207
Now that we have the generic form of $O$, we have to choose values for the constants. The idea here is to work progressively by choosing values that will simplify the equation by removing $X$.
We need to solve :
$$O_0 = bX + cX + dX + eX + a + 18149433503814401207 = 0$$
Choosing $a = -18149433503814401207$ would simplify the equation to :
$$O_0 = bX + cX + dX + eX = 0$$
An obvious solution would be to set every other constant to zero, but this would not be usefull in the long run. Instead of giving exact values, we can constrain them by setting $e = -(b+c+d)$.
# check if O[0] is 0
a = -18149433503814401207
print(O(a=a,e=-(b+c+d))[0])
# 0
We can even check that the vector $O$ will produce a vector $V$ of the correct form after applying R_ :
# check that V is of the correct form
R8 = R_(8, O(a=a,e=-(b+c+d)))
print(R8)
# (297310569895150350, b*X, c*X, d*X, -b*X - c*X - d*X)
Let’s see how the variables will propagate through the next round :
R7 = R_(7, R8)
print(R7[0])
# 18446744073709551546*b*X + 9*c*X + 18446744073709551551*d*X + 13165686892553568318
It would be nice if we could get rid of $X$ from the previous equation, to lower the degree of the final polynomial. For this we can solve $-11b + 9c - 6d = 0 \mod p$, for any variable.
(x, y, z) = var("x,y,z")
print(solve([-11*x + 9*y - 6*z == 0], x)[0])
# x == 9/11*y - 6/11*z
b = Zmod(p)(9)/11 * c - Zmod(p)(6)/11 * d
# check the simplification
print(R7(b=b)[0])
# 13165686892553568318
This added another constraint on our system. Let’s continue with another round.
R6 = R_(6, R7(b=b))
print(R6[0])
# 9922112342677107306*c*X + 18237121981962852068*d*X + 14198193969758665933
We can once again get rid of $X$ by adding a constraint on $c$ :
c = -Zmod(p)(18237121981962852068)/9922112342677107306 * d
# check the simplification
print(R6(c=c)[0])
# 14198193969758665933
Now, our last degree of freedom is on the choice of $d$.
Computing and solving the polynomial
Let’s choose $d = 1$ for simplicity and propagate our vector to the remaining rounds to construct the polynomial $f(x)$ :
# last degree of freedom, propagagte through the remaining rounds
R5 = R_(5, R6(c=c))
print(R5(d=1)[0])
# 9918190068311958073*X + 7452441470924312017
print(R5(d=1)[0].degree())
# 1
R4 = R_(4, R5)
print(R4(d=1)[0].degree())
# 81
R3 = R_(3, R4)
print(R3(d=1)[0].degree())
# 2187
# this took 55s !
R2 = R_(2, R3)
print(R2[0].degree()/2)
# 19683
# this took 8 mins !
R1 = R_(1, R2)
print(R1[0].degree()/2)
# 59049
# this is instant because there is no exponentiation
R0 = R_(0, R1)
print(R0[0].degree()/2)
# 59049
# the polynomial for which we need to find roots
f = R0[0](d=1)
The more we add rounds, the higher the degree becomes and the longer it takes to compute $f(x)$.
Now it’s just a matter of finding the roots.
f = f.univariate_polynomial(PolynomialRing(Zmod(p), names="X", implementation="NTL"))
print(f.roots(multiplicities=False))
But of course, this doesn’t work. I waited an hour, than gave up. Luckily the paper comes to the rescue again with the solution in chapter 3.1.
To compute the roots of our polynomial $P(X) = f(X)$. We first compute another polynomial $Q(X) = X^p - X \mod P$. Then we can compute $R = \text{gcd}(P, Q)$, which will produce a new polynomial of much lower degree, sharing the same roots as $P$. This time, Sage should be able to compute the roots of $R$.
P = f
X = P.variables()[0]
Q = power_mod(X, p, P) - X
R = gcd(P, Q)
print(R)
# X^2 + 12154645665883864359*X + 6369257043859482405
roots = R.roots(multiplicities=False)
print(roots)
# [3897575116405526444, 2394523291420160754]
d. That’s why I kept the variable d until the end.Now it’s just a matter of replacing each variable with its value to find a solution to the CICO problem :
# final check
vD = 1
vX = roots[0]
vB = 14044952737525282753*vD
vC = 16397105843297379163*vB + 12297829382473034372*vD
vE = -vB-vC-vD
O = O(a=a,e=vE,c=vC,b=vB,d=vD,X=vX)
print(O)
# (0, 16576674348004321373, 3322550697993102508, 8561885400519130051, 15728815811707691965)
I = dec(O)
print(I)
# (0, 913035201000614848, 4979648219579392184, 7047076775564669759, 10618636132995750819)
assert enc(I) == O
We can send $I$ to the service and get the flag.
FCSC{449a12ead684fb0162c741fe8575fa94ff43023e4aa4627b9ce7e40cf041b314}
Secret SHenanigans#
Play on HackropoleDifficulty :
Points : 477
Solves : 10
Description :
A crook skilled in technology is wary of proven secure channel protocols like SSH or TLS: “they’re all probably backdoored” he thinks. As he regularly needs to receive confidential information from his colleagues, he has developed his own secure channel establishment protocol, allowing anonymous clients to send confidential information to his server.
You have access to a network TAP positioning you as a Man-in-the-Middle between a client and the server, and you have also managed to grab the application’s source code (unfortunately without the server’s private key…). Can you recover the secret that the client sends to the server?
The service’s source code was provided in an archive :
$ tar -tvf secret-shenanigans.tar.xz
drwxr-xr-x fcsc2024/fcsc2024 0 1970-01-01 00:00 ./public_src/
-rw-r--r-- fcsc2024/fcsc2024 1110 1970-01-01 00:00 ./public_src/Dockerfile
-rw-r--r-- fcsc2024/fcsc2024 91 1970-01-01 00:00 ./public_src/SRC_README.md
-rw-r--r-- fcsc2024/fcsc2024 227 1970-01-01 00:00 ./public_src/Makefile
drwxr-xr-x fcsc2024/fcsc2024 0 1970-01-01 00:00 ./public_src/src/
-rw-r--r-- fcsc2024/fcsc2024 7644 1970-01-01 00:00 ./public_src/src/common.py
-rw-r--r-- fcsc2024/fcsc2024 278 1970-01-01 00:00 ./public_src/src/genserverkeys.py
drwxr-xr-x fcsc2024/fcsc2024 0 1970-01-01 00:00 ./public_src/src/data/
-rw-r--r-- fcsc2024/fcsc2024 46 1970-01-01 00:00 ./public_src/src/data/flag.txt
-rw-r--r-- fcsc2024/fcsc2024 138 1970-01-01 00:00 ./public_src/src/data/server_private_key.der
-rw-r--r-- fcsc2024/fcsc2024 91 1970-01-01 00:00 ./public_src/src/data/server_public_key.der
-rw-r--r-- fcsc2024/fcsc2024 7182 1970-01-01 00:00 ./public_src/src/client.py
-rw-r--r-- fcsc2024/fcsc2024 9881 1970-01-01 00:00 ./public_src/src/sniffer.py
-rw-r--r-- fcsc2024/fcsc2024 4939 1970-01-01 00:00 ./public_src/src/server.py
-rw-r--r-- fcsc2024/fcsc2024 91 1970-01-01 00:00 ./public_src/docker-compose.yml
A README explaining how to use the TAP was also provided. The TAP is set between a client and a server, and it “freezes” the two connection channels
(from server to client and from client to server) whenever one of the two parties sends a packet.
When in TAP mode, it is possible to either:
- Read the two communication buffers.
- Edit these two communication buffers.
- Activate the “always transparent mode from now on” to avoid TAP invocation further away.
- Quit this TAP hook.
There are a lot of source code files, but we will mainly be interested by the code in client.py and server.py. The rest are helper functions and I won’t detail them unless necessary.
Like the description of the challenge indicates, the client and server communicate using a custom protocol. It can be divided into two phases, the first one is the secure channel establishment, where both parties agree upon a shared secret. The second is the secure channel itself, where the server can send encrypted commands to the client. It’s during the secure channel that the server is asking for the flag in an encrypted manner. The goal of the challenge is to find a way to decrypt the response of the client, with MITM capabilities.
Secure channel establishment
Each packet exchanged between the parties is attributed an identifier (CMD_*), which is encoded as a single byte inside the packet.
The first step of the protocol is the exchange of the versions (CMD_STRING_VERSION):
logger.warning("[CLIENT] Spawning the client...")
##### Exchange our version in clear
send_packet_counter = clear_send_packet(send, recv, CMD_STRING_VERSION, CLIENT_VERSION_STRING, send_packet_counter)
cmd, server_version, recv_packet_counter = clear_recv_packet(send, recv, recv_packet_counter, expected_cmd=CMD_STRING_VERSION)
logger.warning(f"[CLIENT] Received server version {server_version}")
##### Proceed with key exchange
# Generate an ephemeral ECDH private key and the corresponding serialized point
x = ECDH_gen_ephemeral_private_key()
Gx = ECDH_gen_public_data(x)
logger.info("[SERVER] Spawning the server")
##### Exchange our version in clear
send_packet_counter = clear_send_packet(send, recv, CMD_STRING_VERSION, SERVER_VERSION_STRING, send_packet_counter)
cmd, client_version, recv_packet_counter = clear_recv_packet(send, recv, recv_packet_counter, expected_cmd=CMD_STRING_VERSION)
logger.info(f"[SERVER] Received client version {client_version.decode()}")
##### Proceed with key exchange
# Generate an ephemeral ECDH private key and the corresponding serialized point
y = ECDH_gen_ephemeral_private_key()
Gy = ECDH_gen_public_data(y)
Each participant keeps count of how many messages they send (send_packet_counter) and receive (recv_packet_counter). They are incremented by the clear_send_packet and clear_recv_packet functions.
This initial exchanges are not encrypted until the secure channel is established.
After this step, both parties generate their ephemeral DH key pairs. $(x, G_x)$ for the client and $(y, G_y)$ for the server.
The server then waits for the client’s public key (CMD_KEXDH_INIT) :
# Wait for something from the client
while True:
cmd, payload, recv_packet_counter = clear_recv_packet(send, recv, recv_packet_counter)
if cmd == CMD_IGNORE:
# In case of ignore command, well ignore and loop ...
logger.info("[SERVER] CMD_IGNORE received")
continue
elif cmd == CMD_PING:
# In case of "ping", respond with "pong" with the received payload and loop
logger.info("[SERVER] CMD_PING received")
send_packet_counter = clear_send_packet(send, recv, CMD_PONG, payload, send_packet_counter)
continue
elif cmd == CMD_KEXDH_INIT:
# In case of key exchange init, this is it we have the data we have been waiting to continue
# the key exchange
logger.info("[SERVER] CMD_KEXDH_INIT received")
break
else:
# This is an unexpected command at this stage
logger.error("[SERVER] Error in possible commands during key exchange. Aborting.")
thread_exit()
The client is allowed to send multiple packets at this point during the protocol.
It can send a CMD_IGNORE packet, that will be received by the server, but no action will be taken, besides incrementing it’s recv_packet_counter.
The client can also send a CMD_PING packet and the server would reply with a CMD_PONG packet. Both participants’ send_packet_counter and recv_packet_counter would be incremented.
The normal behaviour of the client is to simply provide what the server expects, a CMD_KEXDH_INIT packet :
# Send the CMD_KEXDH_INIT to initialize the key exchange
send_packet_counter = clear_send_packet(send, recv, CMD_KEXDH_INIT, Gx, send_packet_counter)
This packet only contains the client’s public key $G_x$.
The client then waits for the server to do the same :
# Wait for a response from the server
while True:
cmd, payload, recv_packet_counter = clear_recv_packet(send, recv, recv_packet_counter)
if cmd == CMD_IGNORE:
logger.warning("[CLIENT] CMD_IGNORE received")
# In case of ignore command, well, ignore and loop...
continue
elif cmd == CMD_PING:
logger.warning("[CLIENT] CMD_PING received")
# In case of "ping", respond with "pong" with the received payload and loop
send_packet_counter = clear_send_packet(send, recv, CMD_PONG, payload, send_packet_counter)
continue
elif cmd == CMD_KEXDH_REPLY:
logger.warning("[CLIENT] CMD_KEXDH_REPLY received")
# In case of key exchange init, this is it we have the data we have been waiting to continue
# the key exchange
break
else:
# This is an unexpected command at this stage
logger.error("[CLIENT] Error in possible commands during key exchange. Aborting.")
thread_exit()
The server can also reply with CMD_IGNORE or CMD_PING, but instead computes the shared secret $s = G_x^y$, and signs the previous transcript using it’s long term private key. It sends it’s ephemeral public key $G_y$ and the signature to the client in a CMD_KEXDH_REPLY packet :
# Here, we compute the shared secret from CMD_KEXDH_INIT
Gx = payload
shared_secret = ECDH_gen_shared_secret(y, Gx)
# Sign the whole key exchange and send the CMD_KEXDH_REPLY
sig = sign_key_exchange(SERVER_VERSION_STRING + client_version + Gx + Gy + server_public_key_raw + shared_secret, server_private_key)
payload_to_send = Gy + sig
send_packet_counter = clear_send_packet(send, recv, CMD_KEXDH_REPLY, payload_to_send, send_packet_counter)
The client verifies the signature, after having computed the shared secret $s = G_y^x$. This however doesn’t introduce any vulnerability in this case.
# Split the payload in its components: ephemeral ECDH public key and ECDSA signature of the key exchange
if len(payload) < 64:
logger.error("[CLIENT] Error in CMD_KEXDH_REPLY payload length. Aborting.")
thread_exit()
Gy, sig = payload[:-64], payload[-64:]
# Here, we compute the shared secret from CMD_KEXDH_REPLY
shared_secret = ECDH_gen_shared_secret(x, Gy)
# Check that the key exchange is indeed OK and that this is the server we are supposed to talk to
check = verify_key_exchange(server_version + CLIENT_VERSION_STRING + Gx + Gy + server_public_key_raw + shared_secret, server_public_key, sig)
if not check:
logger.error("[CLIENT] Error: key exchange signature is not verified. Aborting.")
thread_exit()
# ACK the secure channel establishement by sending CMD_NEWKEYS
send_packet_counter = clear_send_packet(send, recv, CMD_NEWKEYS, b"", send_packet_counter)
If the signature is incorrect, the protocol is aborted. Otherwise, an acknowledgment packet CMD_NEWKEYS is transmitted to the server.
The client could also send CMD_IGNORE packet at this point, but the server will just wait until receiving CMD_NEWKEYS. Once received, it simply acknowledges the establishment as well :
# ACK the secure channel establishement by sending CMD_NEWKEYS
send_packet_counter = clear_send_packet(send, recv, CMD_NEWKEYS, b"", send_packet_counter)
The client also accepts CMD_IGNORE packets before the ackledgment.
At this point a shared secret between the client and server has been established. We’ll see in the next section how it is used to encrypt the communications inside the secure channel.
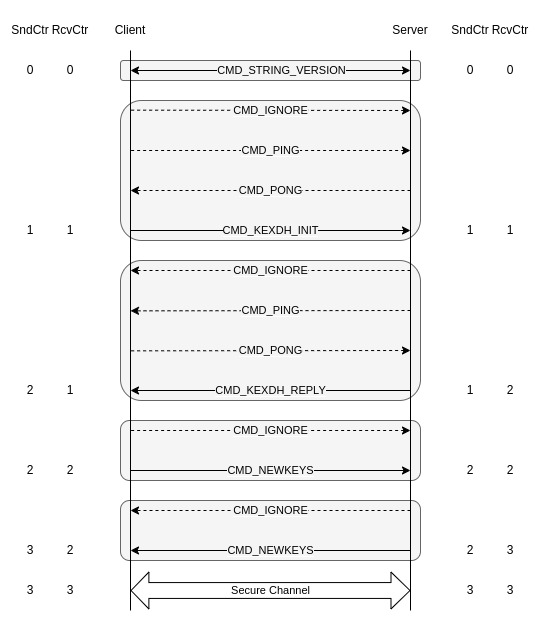
For the moment, there is no obvious vulnerability during this phase of the protocol. From a challenge’s perspective, being able to send unnecessary packets like CMD_IGNORE or CMD_PING is weird, but it shouldn’t matter right ?

Secure channel
Now that both parties share the same secret, encryption can be setup on the client side :
# Derive the secure channel keys
kenc_recv, kmac_recv = derive_secure_channel_keys(b"SERVERTOCLIENT", shared_secret)
kenc_send, kmac_send = derive_secure_channel_keys(b"CLIENTTOSERVER", shared_secret)
# Set secure channel as active
logger.warning("[CLIENT] Secure channel is ON!")
secure_channel = True
iv_recv = INITIAL_RECV_IV # b'\xaa' * 16
iv_send = INITIAL_SEND_IV # b'\xbb' * 16
And on the server side :
# Derive the secure channel keys
kenc_recv, kmac_recv = derive_secure_channel_keys(b"CLIENTTOSERVER", shared_secret)
kenc_send, kmac_send = derive_secure_channel_keys(b"SERVERTOCLIENT", shared_secret)
# Set secure channel as active
logger.info("[SERVER] Secure channel is ON!")
secure_channel = True
iv_recv = INITIAL_RECV_IV # b'\xbb' * 16
iv_send = INITIAL_SEND_IV # b'\xaa' * 16
A pair (key, IV) is derived for both sides of the communication (client->server and server->client).
Let’s first get a good overview of what happens inside the secure channel before diving into the packet encryption.
The client enters a loop and waits for server commands :
# Wait for encrypted commands in secure channel mode, or non-encrypted in non secure channel mode
while True:
if secure_channel:
cmd, payload, recv_packet_counter, iv_recv = sc_recv_packet(send, recv, kenc_recv, kmac_recv, recv_packet_counter, iv_recv)
else:
cmd, payload, recv_packet_counter = clear_recv_packet(send, recv, recv_packet_counter)
# Switch on command received
if cmd == CMD_IGNORE:
# This is an ignore command, well, ignore it!
logger.warning("[CLIENT] CMD_IGNORE received")
continue
elif cmd == CMD_PING:
logger.warning("[CLIENT] CMD_PING received")
resp_cmd = CMD_PONG
payload_to_send = payload
elif cmd == CMD_STRING_VERSION:
logger.warning("[CLIENT] CMD_STRING_VERSION received")
resp_cmd = cmd
payload_to_send = CLIENT_VERSION_STRING
The client accepts known commands like CMD_IGNORE, CMD_PING and CMD_STRING_VERSION, but they are not very interesting.
The first thing that strikes out is that encryption is optional inside the secure channel. It is activated by default, but there is a command to deactivate it CMD_DISABLE_SC :
elif cmd == CMD_DISABLE_SC:
# This can only be excuted when the secure channel is set
logger.warning("[CLIENT] CMD_DISABLE_SC received")
if not secure_channel:
logger.error("[CLIENT] Error: CMD_DISABLE_SC while secure is not active. Aborting.")
thread_exit()
# Disable the secure channel
secure_channel = False
continue
The server never sends this command normally, but maybe we can send it using the TAP.
There is also a command to ask for the flag CMD_GET_FLAG :
elif cmd == CMD_GET_FLAG:
logger.warning("[CLIENT] CMD_GET_FLAG received")
with open("data/flag.txt", "rb") as f:
flag = f.read()
resp_cmd = cmd
payload_to_send = flag
Looks like the plan is to deactivate encryption, then ask for the flag.
There is a last command CMD_SC_SERVER_ADDITIONAL_INFO:
elif cmd == CMD_SC_SERVER_ADDITIONAL_INFO:
# Receive in the secure channel the sensitive data of the server
logger.warning("[CLIENT] CMD_SC_SERVER_ADDITIONAL_INFO received")
if not secure_channel:
logger.error("[CLIENT] Error: CMD_SC_SERVER_ADDITIONAL_INFO while secure is not active. Aborting.")
thread_exit()
continue
This one can only be received when encryption is enabled, but does nothing.
Let’s now look at what the server is doing inside the secure channel.
# Send some sensitive configuration metadata in the secure channel
send_packet_counter, iv_send = sc_send_packet(send, recv, CMD_SC_SERVER_ADDITIONAL_INFO, b"SERVER::will_shutdown_in_2h", kenc_send, kmac_send, send_packet_counter, iv_send)
# Now ask for our secret in secure channel mode
send_packet_counter, iv_send = sc_send_packet(send, recv, CMD_GET_FLAG, b"PLEASE_GIVE_ME_YOUR_SECRET_AS_I_ASK_KINDLY_DEAR_CLIENT!".center(205, b"_"), kenc_send, kmac_send, send_packet_counter, iv_send)
cmd, payload, recv_packet_counter, iv_recv = sc_recv_packet(send, recv, kenc_recv, kmac_recv, recv_packet_counter, iv_recv)
if cmd != CMD_GET_FLAG:
# This is an unexpected response
logger.error("[SERVER] Error: unexpected response at this stage. Aborting.")
thread_exit()
logger.info("[SERVER] Finished our job ... bye!")
The server only sends 2 packets inside the secure channel :
CMD_SC_SERVER_ADDITIONAL_INFO: “SERVER::will_shutdown_in_2h”CMD_GET_FLAG: a very long message
It then expects to receive the flag as a response.
As the TAP allows us to modify or even send additionnal packets, we could intercept the CMD_SC_SERVER_ADDITIONAL_INFO packet and change it by a CMD_DISABLE_SC. That way, the client would send the flag unencrypted. But that’s not as simple as that, messages are encrypted and authenticated. Without the keys, any modification would normally be detected.
It’s time to inspect how the packets are encrypted/decrypted !
Packet encryption
The key derivation is done using SHA-256, but that doesn’t rely matter for the challenge.
Packet encryption/decryption is handled by the sc_send_packet and sc_recv_packet functions.
#### Secure channel communication using Encrypt-then-MAC with established keys
def sc_send_packet(send, recv, cmd_type, payload, kenc, kmac, packet_counter, iv):
# Get the padding to apply
pad = AES.block_size - ((len(payload) + 2) % AES.block_size)
payload = cmd_type + len(payload).to_bytes(1, byteorder = 'big') + payload + (pad * b'\x00')
# Encrypt the padder payload
cipher = AES.new(kenc, AES.MODE_CBC, iv=iv)
payload = cipher.encrypt(payload)
# Compute the HMAC on
h = HMAC.new(kmac, digestmod = SHA256)
if len(payload) + h.digest_size > 255:
logger.error("[ERROR] Payload len is too big")
thread_exit()
prepend = (len(payload) + h.digest_size).to_bytes(1, byteorder = 'big')
# Update with the implicit 64 bits packet counter
h.update(packet_counter.to_bytes(8, byteorder = 'big'))
# Update with the length
h.update(prepend)
h.update(payload)
# Append the HMAC
new_iv = payload[-AES.block_size:]
payload = prepend + payload + h.digest()
# Check the whole length
if len(payload) > 255:
logger.error(f"[ERROR] Payload len {len(payload)} is too big")
thread_exit()
send(payload)
return packet_counter + 1, new_iv
The encryption is done using AES in CBC mode with the key kenc_send and IV iv_send.
The encrypted data is then authenticated using HMAC-SHA256 and the key kmac_send.
send_packet_counter is also part of the authenticated data.
iv_send is updated by taking the last encrypted block, so the encryption stream is chained between packets.
The decryption process starts be verifying the MAC using the key kmac_recv.
If the MAC is correct, the payload is decrypted using AES in CBC mode with IV iv_recv and the key kenc_recv.
iv_recv is updated by taking the last encrypted block, so the encryption stream can be chained between packets.
def sc_recv_packet(send, recv, kenc, kmac, packet_counter, iv, expected_cmd = None):
h = HMAC.new(kmac, digestmod = SHA256)
# Receive the encrypted command length
packet_len_byte = recv(1)
packet_len = int.from_bytes(packet_len_byte, byteorder = 'big')
# Receive the rest
packet = recv(packet_len)
# Packet should be at least MAC plus one block
if len(packet) < (h.digest_size + AES.block_size):
logger.error("[ERROR] Unexpected encrypted packet!")
thread_exit()
# Check the mac
mac = packet[-h.digest_size:]
enc_payload = packet[:-h.digest_size]
new_iv = enc_payload[-AES.block_size:]
# Update with length and packet counter
h.update(packet_counter.to_bytes(8, byteorder = 'big'))
h.update(packet_len_byte)
h.update(enc_payload)
hmac = h.digest()
if hmac != mac:
logger.error("[ERROR] Erroneous MAC in encrypted packet!")
thread_exit()
# MAC is OK, decrypt stuff
cipher = AES.new(kenc, AES.MODE_CBC, iv = iv)
payload = cipher.decrypt(enc_payload)
if len(payload) < 2:
logger.error("[ERROR] Erroneous payload size in encypted packet!")
thread_exit()
cmd = payload[0:1]
if expected_cmd is not None:
if expected_cmd != cmd:
logger.error(f"[ERROR] Unexpected command {expected_cmd} != {cmd}")
thread_exit()
real_len = int.from_bytes(payload[1:2], 'big')
if len(payload[2:]) < real_len:
logger.error("[ERROR] Bad encrypted packet structure")
thread_exit()
payload = payload[2:2 + real_len]
return cmd, payload, packet_counter + 1, new_iv
After decryption, it can be checked that the command is the expected one, but this parameter is never used, so the check is never performed. It is verified that the data length field of the packet is not greater then the length of the decrypted padded data.
Once again, there is no obvious issue in this code besides IV chaining, but this doesn’t seem to be exploitable here.
The challenge’s name hints at SSH. At the end of 2023 this protocol was the subject of a new vulnerability : the Terrapin attack.
By carefully adjusting the sequence numbers during the handshake, an attacker can remove an arbitrary amount of messages sent by the client or server at the beginning of the secure channel without the client or server noticing it.
This is possible because the sequence number counters are not reset at the beginning of the secure channel. As the establishment phase is not integrity protected, a MitM attacker can drop and inject new paquets to manipulate the counters.
Attack plan
Because the attack only allows to drop packets, we can drop the first CMD_SC_SERVER_ADDITIONAL_INFO packet sent by the server at the start of the secure channel. The client would then try to decrypt the CMD_GET_FLAG packet using an incorrect IV, which if interpreted as a CMD_DISABLE_SC packet, would disable encryption. We would then be able to send an unencrypted CMD_GET_FLAG packet to the client and get the flag.
To be able to drop a packet at the start of the secure channel, we have to inject a new packet towards the client during the establishment. This can be achieved by sending a single CMD_IGNORE packet before sending CMD_NEWKEYS.
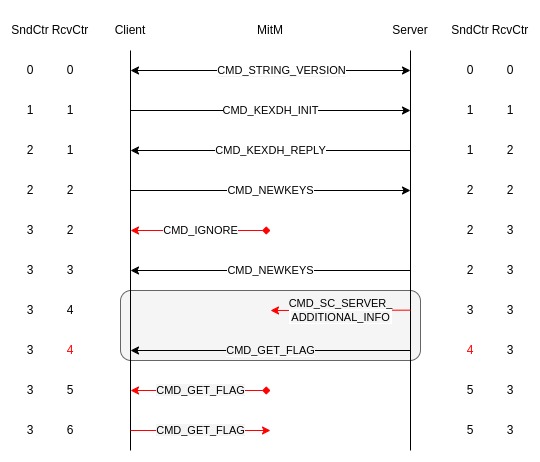
As the packet command is encoded as a single byte, we have $\frac{1}{256}$ chance of obtaining the desired CMD_DISABLE_SC. On top of that, the data length field of the packet must be lower then the length of the decrypted data. Luckily, the CMD_GET_FLAG packet sent by the server has a length of 205. So the chances of a successfull attack are $\frac{1}{256}\cdot\frac{205}{256} = \frac{205}{65536}$, which is about 0.31%. This may not seem like much, but it’s more than enough to make it practically exploitable.
from pwn import *
## Commands
CMD_STRING_VERSION = b"\x00"
CMD_KEXDH_INIT = b"\x01"
CMD_KEXDH_REPLY = b"\x02"
CMD_NEWKEYS = b"\x03"
CMD_IGNORE = b"\x04"
CMD_PING = b"\x05"
CMD_PONG = b"\x06"
CMD_DISABLE_SC = b"\x07"
CMD_SC_SERVER_ADDITIONAL_INFO = b"\x08"
CMD_GET_FLAG = b"\x09"
def readS2C():
conn.sendlineafter(b"actions\n", b"R0")
data = bytes.fromhex(conn.recvline().strip().decode())
return data
def readC2S(timeout=1):
conn.sendlineafter(b"actions\n", b"R1", timeout=timeout)
data = bytes.fromhex(conn.recvline(timeout=timeout).strip().decode())
return data
def writeS2C(data):
conn.sendlineafter(b"actions\n", b"E0"+data.hex().encode())
def writeC2S(data):
conn.sendlineafter(b"actions\n", b"E1"+data.hex().encode())
def next():
conn.sendlineafter(b"actions\n", b"Q")
def buildPacket(cmd, data):
return bytes([len(data)+1]) + cmd + data
with context.silent:
for _ in range(10000):
print(".", end="")
conn = remote("localhost", 4000)
# server version
next()
# client version
next()
# Client KexInit
next()
# Server KexInit
next()
# Client new key
next()
# Server new key
snk = readS2C()
# inject new packet before
p = buildPacket(CMD_IGNORE, b'AAAAAAAAAA')
writeS2C(p+snk)
next()
# ---- secure channel -----
# Server Additionnal info
# drop this packet
writeS2C(b'')
next()
# Server get Flag
sgf = readS2C()
p = buildPacket(CMD_GET_FLAG, b'PP')
writeS2C(sgf+p)
next()
# Client Flag
try:
flag = readC2S(timeout=0.3)
if flag != b'':
print(flag)
conn.close()
except:
conn.close()
It works well locally, with the flag appearing after a few minutes. During the CTF, running the script remotely took a very long time. That’s because the attack implementation is basic and does not handle packet truncation that does happen on the remote instance.
FCSC{1c165d89fadceef1e40d037098a531533150ab871d8d2bff3831c836001a6cce}
Tight Schedule#
Play on HackropoleDifficulty :
Points : 487
Solves : 6
Description :
You must analyze this block cipher engineered by your intern Tuco, el famoso :-)
The following source code was provided :
#!/usr/bin/env python3
import os
import json
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from Crypto.Util.strxor import strxor as xor
class TightSchedule:
S = [
0x63,0x7C,0x77,0x7B,0xF2,0x6B,0x6F,0xC5,0x30,0x01,0x67,0x2B,0xFE,0xD7,0xAB,0x76,
0xCA,0x82,0xC9,0x7D,0xFA,0x59,0x47,0xF0,0xAD,0xD4,0xA2,0xAF,0x9C,0xA4,0x72,0xC0,
0xB7,0xFD,0x93,0x26,0x36,0x3F,0xF7,0xCC,0x34,0xA5,0xE5,0xF1,0x71,0xD8,0x31,0x15,
0x04,0xC7,0x23,0xC3,0x18,0x96,0x05,0x9A,0x07,0x12,0x80,0xE2,0xEB,0x27,0xB2,0x75,
0x09,0x83,0x2C,0x1A,0x1B,0x6E,0x5A,0xA0,0x52,0x3B,0xD6,0xB3,0x29,0xE3,0x2F,0x84,
0x53,0xD1,0x00,0xED,0x20,0xFC,0xB1,0x5B,0x6A,0xCB,0xBE,0x39,0x4A,0x4C,0x58,0xCF,
0xD0,0xEF,0xAA,0xFB,0x43,0x4D,0x33,0x85,0x45,0xF9,0x02,0x7F,0x50,0x3C,0x9F,0xA8,
0x51,0xA3,0x40,0x8F,0x92,0x9D,0x38,0xF5,0xBC,0xB6,0xDA,0x21,0x10,0xFF,0xF3,0xD2,
0xCD,0x0C,0x13,0xEC,0x5F,0x97,0x44,0x17,0xC4,0xA7,0x7E,0x3D,0x64,0x5D,0x19,0x73,
0x60,0x81,0x4F,0xDC,0x22,0x2A,0x90,0x88,0x46,0xEE,0xB8,0x14,0xDE,0x5E,0x0B,0xDB,
0xE0,0x32,0x3A,0x0A,0x49,0x06,0x24,0x5C,0xC2,0xD3,0xAC,0x62,0x91,0x95,0xE4,0x79,
0xE7,0xC8,0x37,0x6D,0x8D,0xD5,0x4E,0xA9,0x6C,0x56,0xF4,0xEA,0x65,0x7A,0xAE,0x08,
0xBA,0x78,0x25,0x2E,0x1C,0xA6,0xB4,0xC6,0xE8,0xDD,0x74,0x1F,0x4B,0xBD,0x8B,0x8A,
0x70,0x3E,0xB5,0x66,0x48,0x03,0xF6,0x0E,0x61,0x35,0x57,0xB9,0x86,0xC1,0x1D,0x9E,
0xE1,0xF8,0x98,0x11,0x69,0xD9,0x8E,0x94,0x9B,0x1E,0x87,0xE9,0xCE,0x55,0x28,0xDF,
0x8C,0xA1,0x89,0x0D,0xBF,0xE6,0x42,0x68,0x41,0x99,0x2D,0x0F,0xB0,0x54,0xBB,0x16
]
RCON = [0x8d, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36]
def __init__(self, key):
self.key = key
self.rk = self.expandKey(self.key)
def _round(self, x, cst = 0):
a, b, c, d = x[-4:]
t = bytes([self.S[b] ^ cst, self.S[c], self.S[d], self.S[a]])
y = xor(x[ 0: 4], t)
y += xor(x[ 4: 8], y[-4:])
y += xor(x[ 8:12], y[-4:])
y += xor(x[12:16], y[-4:])
return y
def expandKey(self, k):
rk = [k]
for _ in range(10):
rk.append(self._round(rk[-1], self.RCON[len(rk)]))
return rk
def encrypt(self, p):
c, sk = p, k
for sk in self.rk[:-1]:
c = xor(c, sk)
for _ in range(5):
c = self._round(c)
return xor(c, self.rk[-1])
k = os.urandom(16)
P = TightSchedule(k)
p = os.urandom(16)
c = P.encrypt(p)
iv = os.urandom(16)
E = AES.new(k, AES.MODE_CBC, iv = iv)
flag = open("flag.txt", "rb").read()
flag_enc = E.encrypt(pad(flag, 16))
print(json.dumps({
"p": p.hex(),
"c": c.hex(),
"iv": iv.hex(),
"flag_enc": flag_enc.hex()
}, indent = 4))
# {
# "p": "0dfa4c6052fb87ef0a8f03f705dd5101",
# "c": "d4ed19e0694101b6b151e11c2db973bf",
# "iv": "cd31cb6e6ded184efbb9a398e31ffdbb",
# "flag_enc": "653ec0cdd7e3a98c33414be8ef07c583d87b876afbff1d960f8f43b5a338e9ff96d87da4406ebe39a439dab3a84697d40c24557cd1ea6f433053451d20ce1fbf191270f4b8cc7891f8779eb615d35c9f"
# }
This wouldn’t be FCSC without a custom block cipher to break. 😉
The TightSchedule class implements a custom block cipher. Judging from it’s name, the key schedule might be vulnerable to something.
We are in possession of a single plaintext/ciphertext pair. The goal is to recover the encryption key. We don’t have access to an oracle to get more pairs.
I usually solve this kind of challenges by threating them as black boxes and tempering with the inputs.
The first thing I tried was inducing differences in a single byte of the plaintext and see how it would influence the ciphertext :
print("Looking for unaffected bytes in the ciphertext:")
for t in range(16):
same = list(range(16))
for _ in range(30):
p2 = list(p)
p2[t] ^= random.randint(0, 255)
p2 = bytes(p2)
P = TightSchedule(k)
c_ = P.encrypt(p2)
for j in range(16):
if c_[j] != c[j] and j in same:
same.remove(j)
print(f"plaintext[{t}] ^= X:\t{same}")
Looking for unaffected bytes in the ciphertext:
plaintext[0] ^= X: [4, 6, 9, 10, 12, 13, 14]
plaintext[1] ^= X: [5, 7, 10, 11, 13, 14, 15]
plaintext[2] ^= X: [4, 6, 8, 11, 12, 14, 15]
plaintext[3] ^= X: [5, 7, 8, 9, 12, 13, 15]
plaintext[4] ^= X: [10, 13, 14]
plaintext[5] ^= X: [11, 14, 15]
plaintext[6] ^= X: [8, 12, 15]
plaintext[7] ^= X: [9, 12, 13]
plaintext[8] ^= X: [4, 6, 12, 14]
plaintext[9] ^= X: [5, 7, 13, 15]
plaintext[10] ^= X: [4, 6, 12, 14]
plaintext[11] ^= X: [5, 7, 13, 15]
plaintext[12] ^= X: []
plaintext[13] ^= X: []
plaintext[14] ^= X: []
plaintext[15] ^= X: []
The result is interesting and proves that the block cipher is not secure. It shows that there are a lot of invariants in the resulting ciphertext, depending on which byte of the plaintext is modified. This is however unexploitable in our context, as we need to recover the key.
That’s why I did the same test, but this time I modified the key :
print("Looking for unaffected bytes in the ciphertext:")
for t in range(16):
same = list(range(16))
for _ in range(30):
k2 = list(k)
k2[t] ^= random.randint(0, 255)
k2 = bytes(k2)
P = TightSchedule(k2)
c_ = P.encrypt(p)
for j in range(16):
if c_[j] != c[j] and j in same:
same.remove(j)
print(f"key[{t}] ^= X:\t{same}")
Looking for unaffected bytes in the ciphertext:
key[0] ^= X: [4, 6, 9, 10, 12, 13, 14]
key[1] ^= X: [5, 7, 10, 11, 13, 14, 15]
key[2] ^= X: [4, 6, 8, 11, 12, 14, 15]
key[3] ^= X: [5, 7, 8, 9, 12, 13, 15]
key[4] ^= X: [10, 13, 14]
key[5] ^= X: [11, 14, 15]
key[6] ^= X: [8, 12, 15]
key[7] ^= X: [9, 12, 13]
key[8] ^= X: [4, 6, 12, 14]
key[9] ^= X: [5, 7, 13, 15]
key[10] ^= X: [4, 6, 12, 14]
key[11] ^= X: [5, 7, 13, 15]
key[12] ^= X: []
key[13] ^= X: []
key[14] ^= X: []
key[15] ^= X: []
The result is exactly the same !
This means that related keys exists for this block cipher and we can distinguish them based on the invariant bytes of the ciphertext.
Searching for related keys
This is a good start but it’s still not enough to be exploitable in practice. In our test, we supposed that only a single byte of the key is incorrect, we just reduced the key space by a single byte.
We can push the idea further and incrementally modify key bytes as long as at least a single byte invariant exists.
From the previous result, we saw that if every byte of the key is correct besides the first one, we have invariants on the indexes 4, 6, 9, 10, 12, 13 and 14 of the ciphertext. If we modify the second byte as well, we are left with indexes 10, 13 and 14. Finally, modifying the first three bytes produces a single invariant on index 14.
Now, depending on which additionnal bytes are modified, we either loose the invariant or keep it. Let’s name the invariant byte index of the ciphertext $u$. We can build the following table :
X = real byte value
key bytes:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 u
. . . X . . X X . X . X X X X X 14
That’s great, we reduced our search space for related keys to $2^{72}$, but that’s still unexploitable for a CTF.

While doing other tests, I found that some bytes of the key are related two by two. For instance if $k_6$ and $k_{14}$ are both wrong by the same difference, the invariant $u$ is unchanged. We can search for those relations between the bytes of the key that can’t be random and end up with :
X = real byte value
A,B = Same XOR difference
? = XOR of difference must be 0
key bytes:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 u
. . . ? . . B ? . A . ? X A B ? 14
Bytes $k_9$ and $k_{13}$ are also related. Bytes $k_3, k_7, k_{11}$ and $k_{15}$ are related in a more complicated manner. They all can be related two by two, but after further testing it turns out that their relation is more complex than that. As long as the XOR of their differences is 0, $u$ isn’t affected. This is huge, because it means that three of them can be completely random and only the last one has to be the right value.
print("Looking for unaffected bytes in the ciphertext:")
same = list(range(16))
for _ in range(30):
k2 = list(k)
A = random.randint(0, 255)
B = random.randint(0, 255)
C = random.randint(0, 255)
D = random.randint(0, 255)
E = random.randint(0, 255)
k2[0] ^= random.randint(0, 255)
k2[1] ^= random.randint(0, 255)
k2[2] ^= random.randint(0, 255)
k2[3] ^= C
k2[4] ^= random.randint(0, 255)
k2[5] ^= random.randint(0, 255)
k2[6] ^= B
k2[7] ^= D
k2[8] ^= random.randint(0, 255)
k2[9] ^= A
k2[10] ^= random.randint(0, 255)
k2[11] ^= E
k2[12] ^= 0
k2[13] ^= A
k2[14] ^= B
k2[15] ^= E^C^D
k2 = bytes(k2)
P = TightSchedule(k2)
c_ = P.encrypt(p)
for j in range(16):
if c_[j] != c[j] and j in same:
same.remove(j)
if len(same) > 0:
print(f"{same}")
With all those relations, we even further decreased the search space. Byte $k_{12}$ is the only one that must be guessed correctly. The chances of finding two pair-wise related bytes is $2^{-8}$ and it’s the same for the 4 related bytes. Thus the chances of finding such a related key are $2^{-(8+8+8+8)} = 2^{-32}$. It’s not a lot, but still in the realms of what’s possible to achieve in a reasonable amount of time using a laptop.
Finding such a related key would immediately reveal $k_{12}$, but would only give partial information on most of the other bytes. However, this is not the only kind of related keys we can find. Let’s name $K_{12}$ the related keys that reveal byte 12. We can apply the same methodology to find three additionnal kinds of related keys : $K_{13}, K_{14}, K_{15}$.
X = real byte value
A,B = Same XOR difference
? = XOR of difference must be 0
key bytes:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 u
. . . ? . . A ? . B . ? X B A ? 14
? . . . ? . . A ? . B . ? X B A 15
. ? . . A ? . . . ? . B A ? X B 12
. . ? . . A ? . B . ? . B A ? X 13
I’ll let you convince yourself that if we can find one related key of each kind, we would reveal the whole key.
The problem we have to solve now is, how do we validate that a key is a related key ?
Distinguishing related keys
A single byte invariant over a single plaintext/ciphertext pair would have a false positive rate of $2^{-8}$, which is way higher than the apparition chances of a related key.
We can write the decryption function and see how a related key affects the result of the decryption :
class TightSchedule:
# ...
def _invRound(self, x, cst = 0):
y = xor(x[ 8:12], x[12:16])
y = xor(x[ 4:8], x[ 8:12]) + y
y = xor(x[ 0:4], x[ 4:8]) + y
a, b, c, d = y[-4:]
t = bytes([self.S[b] ^ cst, self.S[c], self.S[d], self.S[a]])
y = xor(t, x[ 0:4]) + y
return y
def decrypt(self, c):
c = xor(c, self.rk[-1])
for sk in self.rk[:-1][::-1]:
for _ in range(5):
c = self._invRound(c)
c = xor(c, sk)
return c
The following table summarizes the values of $u$ depending on the related key kind and operation performed :
| Operation | $K_{12}$ | $K_{13}$ | $K_{14}$ | $K_{15}$ |
|---|---|---|---|---|
| encrypt | 14 | 15 | 12 | 13 |
| decrypt | 12 | 13 | 14 | 15 |
There is still a single byte invariant, but on a different index $u$. By taking into consideration the encryption and the decryption operations, we can reduce the chance of false positives to $2^{-16}$. That’s better, but still insufficient.
The TightSchedule cipher is composed of 10 rounds in which the _round function is called 5 times. We can see how $u$ changes when working with less encryption/decryption rounds. But first, lets write functions to encrypt/decrypt using only a certain number of rounds :
class TightSchedule:
# ...
def encX(self, p, x):
c = p
for sk in self.rk[:-1-(10-x)]:
c = xor(c, sk)
for _ in range(5):
c = self._round(c)
if x == 10:
c = xor(c, self.rk[-1])
return c
def decX(self, c, x):
if x > 0:
c = xor(c, self.rk[-1])
for sk in self.rk[(10-x):-1][::-1]:
for _ in range(5):
c = self._invRound(c)
c = xor(c, sk)
return c
The following table summarizes the values of $u$ depending on the related key kind and operation performed :
| operation | $K_{12}$ | $K_{13}$ | $K_{14}$ | $K_{15}$ |
|---|---|---|---|---|
| decrypt / decX(10) | 12 | 13 | 14 | 15 |
| encX(1) / decX(9) | 15 | 12 | 13 | 14 |
| encX(2) / decX(8) | 14 | 15 | 12 | 13 |
| encX(3) / decX(7) | 13 | 14 | 15 | 12 |
| encX(4) / decX(6) | 12 | 13 | 14 | 15 |
| encX(5) / decX(5) | 15 | 12 | 13 | 14 |
| encX(6) / decX(4) | 14 | 15 | 12 | 13 |
| encX(7) / decX(3) | 13 | 14 | 15 | 12 |
| encX(8) / decX(2) | 12 | 13 | 14 | 15 |
| encX(9) / decX(1) | 15 | 12 | 13 | 14 |
| encrypt / encX(10) | 14 | 15 | 12 | 13 |
The index $u$ cycles between 15 and 12 in a pattern. we can use that to distinguish a related key with certainty.
def testKey(k, u):
P = TightSchedule(k)
for i in range(11):
p_ = P.encX(p, i)
c_ = P.decX(c, 10-i)
if c_[u] != p_[u]:
return False
u -= 1
if u == 11:
u = 15
return True
The downside of this technique is that it requires at least an encryption and a decryption operation to test a single key. We also have to perform this check 4 different times for each $K_i$.
Because it would take too much time in Python I did it in C during the CTF. But because I’m desperatly looking for an excuse to practice developing in Rust, let’s reimplement the search in this langage instead.

Implementation
// lib.rs
const S: [u8; 256] = [
0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16,
];
const RCON: [u8; 11] = [
0x8d, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36,
];
fn round_func(x: [u8; 16], cst: u8) -> [u8; 16] {
let mut out = [0u8; 16];
out[0] = x[0] ^ S[x[13] as usize] ^ cst;
out[1] = x[1] ^ S[x[14] as usize];
out[2] = x[2] ^ S[x[15] as usize];
out[3] = x[3] ^ S[x[12] as usize];
for i in 4..16 {
out[i] = x[i] ^ out[i - 4];
}
out
}
fn inverse_round(x: [u8; 16], cst: u8) -> [u8; 16] {
let mut out = [0u8; 16];
for i in (4..16).rev() {
out[i] = x[i] ^ x[i - 4];
}
out[0] = x[0] ^ S[out[13] as usize] ^ cst;
out[1] = x[1] ^ S[out[14] as usize];
out[2] = x[2] ^ S[out[15] as usize];
out[3] = x[3] ^ S[out[12] as usize];
out
}
pub fn expand_key(k: [u8; 16]) -> [[u8; 16]; 11] {
let mut rk = [[0u8; 16]; 11];
rk[0] = k;
for i in 1..11 {
rk[i] = round_func(rk[i - 1], RCON[i]);
}
rk
}
pub fn encrypt_rounds(p: [u8; 16], rk: [[u8; 16]; 11], rounds: usize) -> [u8; 16] {
let mut c = p;
for i in 0..rounds {
for j in 0..16 {
c[j] ^= rk[i][j];
}
for _ in 0..5 {
c = round_func(c, 0);
}
}
if rounds == 10 {
for j in 0..16 {
c[j] ^= rk[10][j];
}
}
c
}
pub fn decrypt_rounds(c: [u8; 16], rk: [[u8; 16]; 11], rounds: usize) -> [u8; 16] {
let mut p = c;
if rounds > 0 {
for j in 0..16 {
p[j] ^= rk[10][j];
}
}
for i in ((10 - rounds)..10).rev() {
for _ in 0..5 {
p = inverse_round(p, 0);
}
for j in 0..16 {
p[j] ^= rk[i][j];
}
}
p
}
pub fn decrypt(c: [u8; 16], rk: [[u8; 16]; 11]) -> [u8; 16] {
decrypt_rounds(c, rk, 10)
}
pub fn encrypt(c: [u8; 16], rk: [[u8; 16]; 11]) -> [u8; 16] {
encrypt_rounds(c, rk, 10)
}
// main.rs
use tightschedule;
use rand::Rng;
use std::thread;
// 0dfa4c6052fb87ef0a8f03f705dd5101
const P: [u8; 16] = [
0x0d, 0xfa, 0x4c, 0x60, 0x52, 0xfb, 0x87, 0xef, 0x0a, 0x8f, 0x03, 0xf7, 0x05, 0xdd, 0x51, 0x01,
];
// d4ed19e0694101b6b151e11c2db973bf
const C: [u8; 16] = [
0xd4, 0xed, 0x19, 0xe0, 0x69, 0x41, 0x01, 0xb6, 0xb1, 0x51, 0xe1, 0x1c, 0x2d, 0xb9, 0x73, 0xbf,
];
fn test_key(rk: [[u8; 16]; 11], mut u: usize) -> bool {
for i in 0..11 {
let p_enc = tightschedule::encrypt_rounds(P, rk, i);
let c_dec = tightschedule::decrypt_rounds(C, rk, 10 - i);
if p_enc[u] != c_dec[u] {
return false;
}
u -= 1;
if u == 11 {
u = 15;
}
}
true
}
fn search_related_keys() {
let mut rng = rand::thread_rng();
loop {
let key: [u8; 16] = rng.gen();
let rk = tightschedule::expand_key(key);
for u in 12..=15 {
if test_key(rk, u) {
println!("Found key candidate for index {u}: {:?}", key);
break;
}
}
}
}
pub fn main() {
let mut handles = vec![];
for _ in 0..32 {
let handle = thread::spawn(|| {
search_related_keys();
});
handles.push(handle);
}
for handle in handles {
handle.join().unwrap();
}
}
Where my first implementation in C took about 24h during the CTF (on my old laptop) to give me one related key of each kind, this new one on the new laptop took around 5 minutes.
Found key candidate for index 15: [245, 228, 240, 56, 41, 3, 39, 8, 235, 230, 39, 97, 172, 141, 187, 90]
Found key candidate for index 15: [45, 38, 46, 131, 10, 64, 80, 39, 120, 206, 146, 148, 63, 206, 167, 90]
Found key candidate for index 15: [98, 145, 3, 23, 66, 217, 192, 56, 78, 91, 68, 23, 9, 87, 204, 90]
Found key candidate for index 12: [212, 115, 68, 39, 213, 214, 71, 113, 233, 177, 181, 235, 76, 206, 248, 209]
Found key candidate for index 12: [190, 87, 244, 105, 247, 37, 210, 235, 217, 72, 72, 228, 76, 55, 109, 10]
Found key candidate for index 13: [201, 82, 25, 39, 21, 142, 202, 130, 168, 77, 109, 151, 115, 64, 214, 139]
Found key candidate for index 12: [66, 142, 85, 71, 15, 109, 201, 50, 146, 53, 112, 74, 76, 74, 118, 83]
Found key candidate for index 12: [56, 12, 241, 150, 10, 11, 113, 71, 92, 31, 136, 79, 76, 96, 206, 242]
Found key candidate for index 15: [209, 91, 202, 124, 93, 106, 78, 168, 134, 156, 218, 217, 193, 228, 21, 90]
Found key candidate for index 14: [139, 222, 38, 76, 244, 72, 154, 154, 162, 144, 30, 35, 148, 191, 153, 202]
Now we can reconstruct the original key and decrypt the flag :
from tight import TightSchedule
K15 = bytes([245, 228, 240, 56, 41, 3, 39, 8, 235, 230, 39, 97, 172, 141, 187, 90])
K14 = bytes([139, 222, 38, 76, 244, 72, 154, 154, 162, 144, 30, 35, 148, 191, 153, 202])
K13 = bytes([201, 82, 25, 39, 21, 142, 202, 130, 168, 77, 109, 151, 115, 64, 214, 139])
K12 = bytes([190, 87, 244, 105, 247, 37, 210, 235, 217, 72, 72, 228, 76, 55, 109, 10])
# X = real byte value
# A,B = Same XOR difference
# ? = XOR of difference must be 0
# key bytes:
# 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 u
# . . . ? . . B ? . A . ? X A B ? 14
# ? . . . ? . . A ? . B . ? X B A 15
# . ? . . A ? . . . ? . B A ? X B 12
# . . ? . . A ? . B . ? . B A ? X 13
K = [0]*16
K[15] = K15[15]
K[14] = K14[14]
K[13] = K13[13]
K[12] = K12[12]
B15 = K15[13] ^ K13[13]
D15 = K15[12] ^ K12[12]
D14 = K15[15] ^ K14[15]
B14 = K14[12] ^ K12[12]
D13 = K14[14] ^ K13[14]
C13 = K13[15] ^ K15[15]
C12 = K13[13] ^ K12[13]
B12 = K14[14] ^ K12[14]
K[11] = K14[11] ^ D14
K[10] = K13[10] ^ D13
K[9] = C12 ^ K12[9]
K[8] = D15 ^ K15[8]
K[7] = C13 ^ K13[7]
K[6] = B12 ^ K12[6]
K[5] = B15 ^ K15[5]
K[4] = B14 ^ K14[4]
K[0] = K13[0] ^ (K[4]^K13[4]) ^ (K[8]^K13[8]) ^ (K[12]^K13[12])
K[1] = K14[1] ^ (K[5]^K14[5]) ^ (K[9]^K14[9]) ^ (K[13]^K14[13])
K[2] = K15[2] ^ (K[6]^K15[6]) ^ (K[10]^K15[10]) ^ (K[14]^K15[14])
K[3] = K12[3] ^ (K[7]^K12[7]) ^ (K[11]^K12[11]) ^ (K[15]^K12[15])
p = bytes.fromhex("0dfa4c6052fb87ef0a8f03f705dd5101")
real_c = bytes.fromhex("d4ed19e0694101b6b151e11c2db973bf")
key = bytes(K)
P = TightSchedule(key)
cipher = P.encrypt(p)
if cipher == real_c:
print("Found KEY !!!! : ", key.hex())
iv = bytes.fromhex("cd31cb6e6ded184efbb9a398e31ffdbb")
flag = bytes.fromhex("653ec0cdd7e3a98c33414be8ef07c583d87b876afbff1d960f8f43b5a338e9ff96d87da4406ebe39a439dab3a84697d40c24557cd1ea6f433053451d20ce1fbf191270f4b8cc7891f8779eb615d35c9f")
from Crypto.Cipher import AES
E = AES.new(key, AES.MODE_CBC, iv = iv)
f = E.decrypt(flag)
print(f)
FCSC{1efc507f987a19a5925b85e8dcc78c7011ef22e8f23bd7ebadf6aff3ed1416f9}

Conclusion#
There was quite a lot of challenges this year and I found them quite difficult, as expected for a 9-day competition. Interstingly, I found the two-star challenges easier than (or as difficult as) some of the one-star challenges. I guess I was not the only one to feel this way judging by the number of solves.
Anyway, it was quite enjoyable and educational, as usual. Looking forward to next year ! 😉